Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-25T05:54:47.723Z Has data issue: false hasContentIssue false
  • English
  • Français

Effective results for points on certain subvarieties of tori

Published online by Cambridge University Press:  01 July 2009

ATTILA BÉRCZES ,
KÁLMÁN GYŐRY ,
JAN-HENDRIK EVERTSE  and
CORENTIN PONTREAU
ATTILA BÉRCZES
Affiliation:
Institute of Mathematics, University of Debrecen, Number Theory Research Group, Hungarian Academy of Sciences and University of Debrecen, H-4010 Debrecen, P.O. Box 12, Hungary. e-mail: [email protected], [email protected]
KÁLMÁN GYŐRY
Affiliation:
Institute of Mathematics, University of Debrecen, Number Theory Research Group, Hungarian Academy of Sciences and University of Debrecen, H-4010 Debrecen, P.O. Box 12, Hungary. e-mail: [email protected], [email protected]
JAN-HENDRIK EVERTSE
Affiliation:
Universiteit Leiden, Mathematisch Instituut, Postbus 9512, 2300 RA Leiden, The Netherlands. e-mail: [email protected]
CORENTIN PONTREAU
Affiliation:
Laboratoire de Mathématiques Nicolas Oresme CNRS UMR 6139, Université de Caen, 14032 Caen cedex, France. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The combined conjecture of Lang-Bogomolov for tori gives an accurate description of the set of those points x of a given subvariety 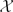of 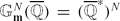, that with respect to the height are “very close” to a given subgroup Γ of finite rank of 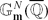. Thanks to work of Laurent, Poonen and Bogomolov, this conjecture has been proved in a more precise form.

In this paper we prove, for certain special classes of varieties 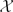, effective versions of the Lang-Bogomolov conjecture, giving explicit upper bounds for the heights and degrees of the points x under consideration. The main feature of our results is that the points we consider do not have to lie in a prescribed number field. Our main tools are Baker-type logarithmic forms estimates and Bogomolov-type estimates for the number of points on the variety 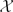with very small height.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 147 , Issue 1 , July 2009 , pp. 69 - 94
Copyright
Copyright © Cambridge Philosophical Society 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bérczes, A., Evertse, J.-H. and Györy, K. Effective results for linear equations in two unknowns from a multiplicative division group. Acta Arith., to appear.Google Scholar
[2]Beukers, F. and Zagier, D.Lower bounds of heights of points on hypersurfaces. Acta Arith. 79 (1997), 103–111.CrossRefGoogle Scholar
[3]Bombieri, E. and Gubler, W.Heights in Diophantine Geometry (Cambridge University Press, 2006).Google Scholar
[4]Bombieri, E. and Zannier, U.Algebraic points on subvarieties of , Internat. Math. Res. Notices 7 (1995), 333–347.CrossRefGoogle Scholar
[5]Borosh, I., Flahive, M., Rubin, D. and Treybig, B.A sharp bound for solutions of linear Diophantine equations. Proc. Amer. Math. Soc. 105 (1989), 844–846.CrossRefGoogle Scholar
[6]David, S. and Philippon, P.Minorations des hauteurs normalisées des sous-variétés de variétés abeliennes. II. Comment. Math. Helv. 77 (2002), 639–700.Google Scholar
[7]Evertse, J.-H. Points on subvarieties of tori. In: A panorama of number theory or the view from Baker's garden (Zürich, 1999) (Cambridge University Press, 2002), pp. 214–230.CrossRefGoogle Scholar
[8]Laurent, M.Equations diophantiennes exponentielles. Invent. Math. 78 (1984), 299–327.CrossRefGoogle Scholar
[9]Liardet, P.Sur une conjecture de Serge Lang. Astérisque 24–25, (1975), 187–210.Google Scholar
[10]Pontreau, C. Petits points d'une surface. Canad J. of Math., to appear.Google Scholar
[11]Pontreau, C. A Mordell–Lang plus Bogolomov type result for curves in . Monatsh. Math. to appear.Google Scholar
[12]Poonen, B.Mordell–Lang plus Bogomolov. Invent. Math. 137 (1999), 413–425.CrossRefGoogle Scholar
[13]Rémond, G.Sur les sous-variétés des tores. Compositio Math. 134 (2002), 337–366.CrossRefGoogle Scholar
[14]Schlickewei, H. P.Lower bounds for heights on finitely generated groups. Monatsh. Math. 123 (1997), 171–178.CrossRefGoogle Scholar
[15]Schmidt, W. M. Heights of points on subvarieties of . In Number Theory (Paris, 1993–1994), London Math. Soc. Lecture Note Ser. 235 (Cambridge University Press, 1996), 157–187.CrossRefGoogle Scholar
[16]Voutier, P.An effective lower bound for the height of algebraic numbers. Acta Arith. 74 (1996), 81–95.Google Scholar
[17]Zhang, S.Positive line bundles on arithmetic varieties. J. Amer. Math. Soc. 8 (1995), 187–221.Google Scholar