Article contents
Divisors computing minimal log discrepancies on lc surfaces
Published online by Cambridge University Press: 14 February 2023
Abstract
Let
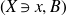 $(X\ni x,B)$
be an lc surface germ. If
$(X\ni x,B)$
be an lc surface germ. If
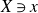 $X\ni x$
is klt, we show that there exists a divisor computing the minimal log discrepancy of
$X\ni x$
is klt, we show that there exists a divisor computing the minimal log discrepancy of
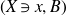 $(X\ni x,B)$
that is a Kollár component of
$(X\ni x,B)$
that is a Kollár component of
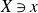 $X\ni x$
. If
$X\ni x$
. If
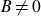 $B\not=0$
or
$B\not=0$
or
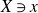 $X\ni x$
is not Du Val, we show that any divisor computing the minimal log discrepancy of
$X\ni x$
is not Du Val, we show that any divisor computing the minimal log discrepancy of
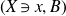 $(X\ni x,B)$
is a potential lc place of
$(X\ni x,B)$
is a potential lc place of
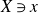 $X\ni x$
. This extends a result of Blum and Kawakita who independently showed that any divisor computing the minimal log discrepancy on a smooth surface is a potential lc place.
$X\ni x$
. This extends a result of Blum and Kawakita who independently showed that any divisor computing the minimal log discrepancy on a smooth surface is a potential lc place.
MSC classification
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 175 , Issue 1 , July 2023 , pp. 107 - 128
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Cambridge Philosophical Society
References
- 1
- Cited by


