Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-30T17:15:33.689Z Has data issue: false hasContentIssue false
  • English
  • Français

Distinguishing endpoint sets from Erdős space

Part of: Special properties Complex dynamical systems Entire and meromorphic functions, and related topics

Published online by Cambridge University Press:  15 February 2022

DAVID S. LIPHAM
DAVID S. LIPHAM*
Affiliation:
Department of Mathematics, Auburn University at Montgomery, Montgomery AL 36117, U.S.A. e-mails: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that the set of all endpoints of the Julia set of 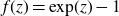$f(z)=\exp\!(z)-1$ which escape to infinity under iteration of f is not homeomorphic to the rational Hilbert space 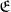$\mathfrak E$ . As a corollary, we show that the set of all points 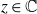$z\in \mathbb C$ whose orbits either escape to 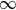$\infty$ or attract to 0 is path-connected. We extend these results to many other functions in the exponential family.

MSC classification

Primary: 37F10: Polynomials; rational maps; entire and meromorphic functions
Secondary: 30D05: Functional equations in the complex domain, iteration and composition of analytic functions 54F50: Spaces of dimension $leq 1$; curves, dendrites
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 173 , Issue 3 , November 2022 , pp. 635 - 646
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Cambridge Philosophical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aarts, J. M. and Oversteegen, L. G.. The geometry of Julia sets. Trans. Amer. Math. Soc. 338 (1993), no. 2, 897–918.10.1090/S0002-9947-1993-1182980-3CrossRefGoogle Scholar
Alhabib, N. and Rempe-Gillen, L.. Escaping endpoints explode. Comput. Methods Funct. Theory 17, 1 (2017), 65–100.CrossRefGoogle Scholar
Alhamed, M., Rempe, L. and Sixsmith, D.. Geometrically finite transcendental entire functions, preprint https://arxiv.org/abs/2003.08884.Google Scholar
Dijkstra, J. J. and Lipham, D. S.. On cohesive almost zero-dimensional spaces, to appear in Canad. Math. Bull.Google Scholar
Dijkstra, J. J. and van Mill, J.. Erdős space and homeomorphism groups of manifolds. Mem. Amer. Math. Soc. 208 (2010), no. 979.Google Scholar
Devaney, R. L. and Krych, M.. Dynamics of $\exp\!(z)$ . Ergodic Theory Dynam. Systems 4 (1984), 35–52.CrossRefGoogle Scholar
Erdős, P., The dimension of the rational points in Hilbert space. Ann. of Math. (2) 41 (1940),734–736.CrossRefGoogle Scholar
Eremenko, A. E. and Lyubich, M. Y.. Dynamical properties of some classes of entire functions. Ann. Inst. Fourier (Grenoble) 42 (1992), no. 4, 989–1020.CrossRefGoogle Scholar
Evdoridou, V. and Rempe–Gillen, L.. Non-escaping endpoints do not explode. Bull. London Math. Soc. 50(5) (2018) pp. 916–932.CrossRefGoogle Scholar
KarpiŃska, B.. Hausdorff dimension of the hairs without endpoints for $\lambda \exp z$ . C. R. Acad. Sci. Paris Ser. I Math. 328 (1999), 1039–1044.CrossRefGoogle Scholar
Kawamura, K., Oversteegen, L. G. and Tymchatyn, E. D.. On homogeneous totally disconnected 1-dimensional spaces. Fund. Math. 150 (1996), 97–112.CrossRefGoogle Scholar
Lipham, D. S.. A note on the topology of escaping endpoint. Ergodic Theory Dynam. Systems. 41(4), 1156–1159.CrossRefGoogle Scholar
Lipham, D. S.. The topological dimension of radial Julia set. Computational Method Funct. Theory, to appear.Google Scholar
Lipham, D. S.. Erdős space in Julia sets, preprint https://arxiv.org/pdf/2004.12976.pdf.Google Scholar
Lipham, D. S.. Another almost zero-dimensional space of exact multiplicative class 3, preprint https://arxiv.org/abs/2010.13876.Google Scholar
Mayer, J. C.. An explosion point for the set of endpoints of the Julia set of exp(z). Ergodic Theory Dynam. Systems 10 (1990), 177–183.CrossRefGoogle Scholar
McMullen, C.. Area and Hausdorff dimension of Julia sets of entire functions. Trans. Amer. Math. Soc. 300 (1987), 329–342.CrossRefGoogle Scholar
Nadler, S. B. Jr. Continuum theory: an introduction. Pure Appl. Math., vol. 158 (Marcel Dekker, Inc., New York, 1992).Google Scholar
Rempe, L.. Topological dynamics of exponential maps on their escaping sets. Ergodic Theory Dynam Systems 26(6) (2006), 1939–1975.CrossRefGoogle Scholar