Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-24T17:11:45.288Z Has data issue: false hasContentIssue false
  • English
  • Français

The definition of measure in function space

Published online by Cambridge University Press:  24 October 2008

H. R. Pitt
H. R. Pitt
Affiliation:
Queen's UniversityBelfast
Get access Rights & Permissions [Opens in a new window]

Extract

A fundamental result in the theory of measure in the space Ω of real functions x(t) of a real variable t is the following theorem of Kolmogoroff:

Theorem 1. Suppose that functions F(t1, …, tn; b1 …, bn) = F(t; b) are defined for positive integers n and real numbers t1, …, tn, b1, …, bn, and have the following properties:

(1·1) For every fixedt1, …, tn, F(t; b) has non-negative differences

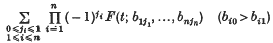
with respect to the variables bl, b2,…, bn, and is continuous on the right with respect to each of them;

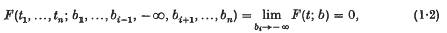
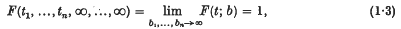
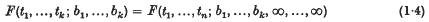
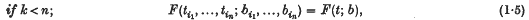
if (i1, …, in) is any permutation of (1, 2, …, n). Then a measure P(X) can be defined in a Borel system of subsets of Ω in such a way that the set of functions satisfying

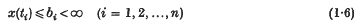
is measurable for any realbi, tiand has measure F(t; b).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 46 , Issue 1 , January 1950 , pp. 19 - 27
Copyright
Copyright © Cambridge Philosophical Society 1950

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Doob, J. L.Stochastic processes depending on continuous parameter. Trans. American Math. Soc. 42 (1937), 107–40.CrossRefGoogle Scholar
(2)Doob, J. L.Regularity properties of certain families of chance variables. Trans. American Math. Soc. 47 (1940), 455–86.CrossRefGoogle Scholar
(3)Doob, J. L.Probability in function space. Bull. American Math. Soc. 53 (1947), 15–30.CrossRefGoogle Scholar
(4)Kakutani, S.Notes on infinite product measure spaces. Proc. Imp. Acad. Tokyo, 19 (1943), 184–8.Google Scholar
(5)Khintchine, A.Asymptotische Gesetze der Wahrscheinlichkeitsrechnung. Ergebn. Math. 2 (1933), no. 4.Google Scholar
(6)Kolmogoroff, A.Grundbegriffe der Wahrscheinlichkeitsrechnung. Ergebn. Math. 2 (1933), no. 3.Google Scholar