Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-25T02:12:56.679Z Has data issue: false hasContentIssue false
  • English
  • Français

The Coxeter–Todd lattice, the Mitchell group, and related sphere packings

Published online by Cambridge University Press:  24 October 2008

J. H. Conway  and
N. J. A. Sloane
J. H. Conway
Affiliation:
University of Cambridge
N. J. A. Sloane
Affiliation:
Mathematics and Statistics Research Center, Bell Laboratories, Murray Hill, New Jersey 07974, USA
Get access Rights & Permissions [Opens in a new window]

Extract

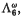This paper studies the Coxeter–Todd lattice its automorphism group (which is Mitchell's reflection group 6·PSU(4, 3)·2), and the associated 12-dimensional real lattice K12. We give several constructions for 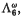, which is a Z[ω]-lattice where ω = e2πi/3; enumerate the congruence classes of 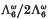and where θ = ω − ω¯; prove the lattice is unique; determine its covering radius and deep holes; and study its connections with the lattice E6 and the Leech lattice. A number of new dense lattices in dimensions up to about 107 are constructed. We also give an explicit basis for the invariants of the Mitchell group. The paper concludes with an extensive bibliography.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 93 , Issue 3 , May 1983 , pp. 421 - 440
Copyright
Copyright © Cambridge Philosophical Society 1983

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Barnes, E. S. and Sloane, N. J. A.New lattice packings of spheres. Canad. J. Math. 35 (1983) 117–130.CrossRefGoogle Scholar
(2)Benard, M.Characters and Schur indices of the unitary reflection group [3 2 1]3. Pacific J. Math. 58 (1975) 309–321.CrossRefGoogle Scholar
(3)Bos, A., Conway, J. H. and Sloane, N. J. A.Further lattice packings in high dimensions. Mathematika 29 (1982) 171–180.CrossRefGoogle Scholar
(4)Bourbaki, N.Groupes et algèbres de Lie, chap. 4–6 (Hermann, Paris, 1968).Google Scholar
(5)Bruen, A. A. and Hirschfeld, J. W. P.Applications of line geometry over finite fields. II. The Hermitian surface. Geometriae Dedicata 7 (1978) 333–353, esp. p. 340.CrossRefGoogle Scholar
(6)Carter, R.Simple groups of Lie type (Wiley, New York 1972).Google Scholar
(7)Chevalley, C.Invariants of finite groups generated by reflections. Amer. J. Math. 67 (1955) 778–782.CrossRefGoogle Scholar
(8)Cohen, A. M.Finite complex reflection groups. Ann. Sci. Ecole Norm. Sup. 9 (1976), 379–436.CrossRefGoogle Scholar
(9)Conway, J. H.A group of order 8,315,553,613,086,720,000. Bull. Lond. Math. Soc. 1 (1969) 79–88.CrossRefGoogle Scholar
(10)Conway, J. H.A characterisation of Leech's lattice. Inventiones math. 7 (1969) 137–142.CrossRefGoogle Scholar
(11)Conway, J. H. Three lectures on exceptional groups. In Finite simple groups, ed. Powell, M. B. and Higman, G. (Academic Press, New York 1971), pp. 215–247.Google Scholar
(12)Conway, J. H. The miracle octad generator. In Topics in group theory and computation, ed. Curran, M. P. J. (Academic Press, New York 1977), pp. 62–68.Google Scholar
(13)Conway, J. H., Parker, R. A. and Sloane, N. J. A.The covering radius of the Leech lattice. Proc. Royal Soc. London, Ser. A, 380 (1982) 261–290.Google Scholar
(14)Conway, J. H., Pless, V. and Sloane, N. J. A.Self-dual codes over GF(3) and GF(4) of length not exceeding 16. IEEE Trans. Information Theory IT-25 (1979) 312–322.CrossRefGoogle Scholar
(15)Conway, J. H. and Sloane, N. J. A.On the enumeration of lattices of determinant one. J. Number Theory 15 (1982) 83–94.CrossRefGoogle Scholar
(16)Conway, J. H. and Sloane, N. J. A.Fast quantizing and decoding algorithms for lattice quantizers and codes. IEEE Trans. Information Theory IT-28 (1982) 227–232.CrossRefGoogle Scholar
(17)Conway, J. H. and Sloane, N. J. A.Laminated lattices. Ann. of Math. 116 (1982) 593–620.CrossRefGoogle Scholar
(18)Conway, J. H. and Sloane, N. J. A.Complex and integral laminated lattices. Trans. Amer. Math. Soc. (in the Press.)Google Scholar
(19)Conway, J. H. and Sloane, N. J. A. On the Voronoi regions of certain lattices. (In preparation.)Google Scholar
(20)Coxeter, H. S. M.The product of the generators of a finite group generated by reflections. Duke Math. J. 18 (1951) 765–782.CrossRefGoogle Scholar
(21)Coxeter, H. S. M.Finite groups generated by unitary reflections. Abh. Math. Sem. Univ. Hamburg 31 (1967) 125–135.CrossRefGoogle Scholar
(22)Coxeter, H. S. M.Regular complex polytopes. (Cambridge University Press 1974).Google Scholar
(23)Coxeter, H. S. M. and Todd, J. A.An extreme duodenary form. Canad. J. Math. 5 (1953), 384–392.CrossRefGoogle Scholar
(24)Curtis, R. T.On subgroups of.0. I: Lattice stabilizers. J. Algebra, 27 (1973) 549–573.CrossRefGoogle Scholar
(25)Dickson, L. E.Linear groupe with an exposition of the Galois field theory (reprinted by Dover Publications, New York 1958).Google Scholar
(26)Dieudonné, J. A.La géométrie des groupes classiques, 3rd ed. (Springer-Verlag, New York, 1971), esp. p. 109.Google Scholar
(27)Edge, W. L.The geometry of an orthogonal group in six variables. Proc. Lona. Math. Soc. 8 (1958) 416–446.CrossRefGoogle Scholar
(28)Edge, W. L.The partitioning of an orthogonal group in six variables. Proc. Roy. Soc. London, Ser. A, 247 (1958) 539–549.Google Scholar
(29)Feit, W.Some lattices over Q(√−3). J. Algebra 52 (1978) 248–263.CrossRefGoogle Scholar
(30)Flatto, L.Basic sets of invariants for finite reflection groups. Bull. Amer. Math. Soc. 74 (1968) 730–734.CrossRefGoogle Scholar
(31)Flatto, L.Invariants of finite reflection groups and mean value problems. II. Amer. J. Math. 92 (1970) 552–561.CrossRefGoogle Scholar
(32)Flatto, L.Invariants of finite reflection groups. L'Enseignement Math. 24 (1978) 237–292.Google Scholar
(33)Flatto, L. and Wiener, M. M.Invariants of finite reflection groups and mean value problems. Amer. J. Math. 91 (1969) 591–598.CrossRefGoogle Scholar
(34)Flatto, L. and Wiener, M. M.Regular polytopes and harmonic polynomials. Canad. J. Math. 22 (1970) 7–21.CrossRefGoogle Scholar
(35)Gorenstein, D.The classification of finite simple groups. I. Simple groups and local analysis. Bull. Amer. Math. Soc. 1 (1979) 43–199.CrossRefGoogle Scholar
(36)Gorenstein, D.Finite simple groups (Plenum, New York 1982).CrossRefGoogle Scholar
(37)Hamill, C. M.On a finite group of order 6,531,840. Proc. Lond. Math. Soc. 52 (1951), 401–454.Google Scholar
(38)Hartley, E. M.A sextic primal in five dimensions. Proc. Cambridge Philos. Soc. 46 (1950), 91–105.CrossRefGoogle Scholar
(39)Hartley, E. M.Two maximal subgroups of a collineation group in five dimensions. Proc. Cambridge Philos. Soc. 46 (1950) 555–569.CrossRefGoogle Scholar
(40)Kantor, W. M. Generation of linear groups. In The geometric vein: The Coxeter festchrift, ed. Davis, C. et al. (Springer-Verlag, New York 1981), pp. 497–509.CrossRefGoogle Scholar
(41)Leech, J. and Sloane, N. J. A.Sphere packing and error-correcting codes. Canad. J. Math. 23 (1971) 718–745.CrossRefGoogle Scholar
(42)Lindsey, J. H. II. A correlation between PSU4(3), the Suzuki group, and the Conway group. Trans. Amer. Math. Soc. 157 (1971) 189–204.CrossRefGoogle Scholar
(43)Lindsey, J. H. II. Finite linear groups of degree six. Canad. J. Math. 5 (1971) 771–790.CrossRefGoogle Scholar
(44)MacWilliams, F. J., Odlyzko, A. M., Sloane, N. J. A. and Ward, H. N.Self-dual codes over GF(4). J. Combinatorial Theory, A 25 (1978) 288–318.CrossRefGoogle Scholar
(45)Mathlab Group, Macsyma Reference Manual (Laboratory for Computer Science, M.I.T., Cambridge, MA, Version 9 1977).Google Scholar
(46)Mitchell, H. H.Determination of all primitive collineation groups in more than four variables. Amer. J. Math. 36 (1914) 1–12.CrossRefGoogle Scholar
(47)Niemeier, H.-V.Definite quadratische Formen der Dimension 24 und Diskriminante 1. J. Number Theory 5 (1973) 142–178.CrossRefGoogle Scholar
(48)Norton, S.A bound for the covering radius of the Leech lattice. Proc. Roy. Soc. London, Ser. A, 380 (1982) 259–260.Google Scholar
(49)Shephard, G. C.Unitary groups generated by reflections. Canad. J. Math. 5 (1953) 364–383.CrossRefGoogle Scholar
(50)Shephard, G. C. and Todd, J. A.Finite unitary reflection groups. Canad. J. Math. 6 (1954), 274–304.CrossRefGoogle Scholar
(51)Sloane, N. J. A.Error-correcting codes and invariant theory: new applications of a nineteenth-century technique. Amer. Math. Monthly 84 (1977) 82–107.CrossRefGoogle Scholar
(52)Sloane, N. J. A.Codes over GF(4) and complex lattices. J. Algebra 52 (1978) 168–181.CrossRefGoogle Scholar
(53)Sloane, N. J. A. Self-dual codes and lattices. In Relations between combinatorics and other parts of mathematics. Proc. Sympos. Pure Math. vol. xxxiv (Amer. Math. Soc., Providence, Rhode Island 1979), pp. 273–308.CrossRefGoogle Scholar
(54)Sloane, N. J. A.Tablee of sphere packings and spherical codes. IEEE Trans. Information Theory IT-27 1981) 327–338.CrossRefGoogle Scholar
(55)Springer, T. A.Invariant theory. Lecture Notes Math. 585 (Springer-Verlag, New York, 1977).CrossRefGoogle Scholar
(56)Stanley, R. P.Invariants of finite groups and their applications to combinatorics. Bull. Amer. Math. Soc. 1 (1979) 475–511.CrossRefGoogle Scholar
(57)Tits, J. Classification of algebraic semisimple groups. In Algebraic groups and discontinuous subgroups, Proc. Sympos. Pure Math. vol. IX (Amer. Math. Soc., Providence, Rhode Island 1966), pp. 33–62.CrossRefGoogle Scholar
(58)Todd, J. A.The invariants of a finite collineation group in five dimensions. Proc. Cambridge Philos. Soc. 46 (1950) 73–90.CrossRefGoogle Scholar
(59)Todd, J. A.The characters of a collineation group in five dimensions. Proc. Boy. Soc. London, Ser. A 200 (1950) 320–336.Google Scholar
(60)Wilson, R. A. The complex Leech lattice and maximal subgroups of the Suzuki group. J. Algebra (in the Press).Google Scholar
(61)Wilson, R. A. The maximal subgroups of Conway's group Co1. J. Algebra (in the Press).Google Scholar