Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T12:48:25.850Z Has data issue: false hasContentIssue false
  • English
  • Français

Continuity properties of compact right topological groups

Published online by Cambridge University Press:  24 October 2008

Paul Milnes
Paul Milnes
Affiliation:
University of Western Ontario
Get access Rights & Permissions [Opens in a new window]

Abstract

Compact right topological groups appear naturally in topological dynamics. Some continuity properties of the one arising as an enveloping semigroup from the distal function 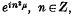are considered here (and, by way of comparison, the enveloping semigroups arising from two almost automorphic functions are discussed). The continuity properties are established either explicitly or by citing a theorem which is proved here and gives some characterizations of almost periodic functions. One characterization is proved using the result (essentially due to W. A. Veech) that a distal, almost automorphic function is almost periodic. A proof of this last result is also given.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 86 , Issue 3 , November 1979 , pp. 427 - 435
Copyright
Copyright © Cambridge Philosophical Society 1979

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Auslander, J. and Hahn, F.oint transitive flows, algebras of functions and the Bebutov system. Fund. Math. 60 (1967), 117–137.CrossRefGoogle Scholar
(2)Auslander, L. and Hahn, F.eal functions coming from flows on compact spaces and concepts of almost periodicity. Trans. Amer. Math. Soc. 106 (1963), 415–426.CrossRefGoogle Scholar
(3)Berglund, J. F., Junghenn, H. D. and Milnes, P. Semigroup Compactifications and Generalizations of Almost Periodicity. Lecture Notes in Mathematics 663 (Springer, New York, 1978).Google Scholar
(4)Ellis, R.Locally compact transformation groups. Duke Math. J. 24 (1957), 119–125.CrossRefGoogle Scholar
(5)Ellis, R.Lectures on Topological Dynamics (New York, Benjamin, 1969).Google Scholar
(6)Flor, P.Rhythmische Abbildungen abelscher Gruppen II. Z. Wahrscheinlichkeitstheorie und Verw. Gebiete 7 (1967), 17–28.CrossRefGoogle Scholar
(7)Furstenberg, H.Strict ergodicity and transformation of the torus. Amer. J. Math. 83 (1961), 573–601.CrossRefGoogle Scholar
(8)Furstenberg, H.The structure of distal flows. Amer. J. Math. 85 (1963), 477–515.CrossRefGoogle Scholar
(9)Hardy, G. H. and Littlewood, J. E.Some problems of diophantine approximation. Acta Math. 37 (1914), 155–191.CrossRefGoogle Scholar
(10)Hewitt, E. and Ross, K. A.Abstract Harmonic Analysis, vol. i (New York, springer, 1963).Google Scholar
(11)Knapp, A. W.Distal functions on groups. Trans. Amer. Math. Soc. 128 (1967), 1–40.CrossRefGoogle Scholar
(12)Knapp, A. W.Functions behaving like almost automorphic functions, pp. 299–317 in Topological Dynamics, an International Symposium, Benjamin (New York, 1968).Google Scholar
(13)Lawson, J. D.Joint continuity in semitopological semigroups. Illinois J. Math. 18 (1973), 275–285.Google Scholar
(14)Milnes, P.Almost automorphic functions and totally bounded groups. Rocky Mountain Math. J. 7 (1977), 231–250.CrossRefGoogle Scholar
(15)Milnes, P. and Pym, J. S.Counterexample in the theory of continuous functions on topological groups. Pacific J. Math. 66 (1976), 205–209.CrossRefGoogle Scholar
(16)Namioka, I.Right topological groups, distal flows and a fixed point theorem, Math. Systems Theory 6 (1972), 193–209.CrossRefGoogle Scholar
(17)Namioka, I.Separate continuity and joint continuity, Pacific J. Math. 51 (1974), 515–531.CrossRefGoogle Scholar
(18)Ruppert, W.Rechtstopologische Halbgruppen. J. Heine Angew. Math. 261 (1973), 123–133.Google Scholar
(19)Ruppert, W.Über kompakte rechtstopologisohe Gruppen mit gleichgradig stetigen Links-translationen. Am. Österreich. Akad. Wiss. Math. – Naturw. Kl. 184 (1975), 159–169.Google Scholar
(20)Ruppert, W.Notes on compact semigroups with identity. Semigroup Forum 14 (1977), 199–234.CrossRefGoogle Scholar
(21)Ruppert, W. On semigroup compactifications of topological groups.Google Scholar
(22)Terras, R. Almost automorphic functions on tcpological groups, Thesis, Univ. of Illinois, 1970.Google Scholar
(23)Veech, W. A.Almost automorphic functions on groups. Amer. J. Math. 87 (1965), 719–751.CrossRefGoogle Scholar