No CrossRef data available.
The consistency of cardinal series
Published online by Cambridge University Press: 24 October 2008
Extract
1. Whittaker (7), generalizing a result of Ferrar(3), showed that the cardinal series based on the positive and negative integers is consistent in the sense that, if
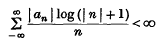
and an integral function f (x) is denned by
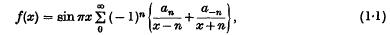
then provided 0 < λ > 1
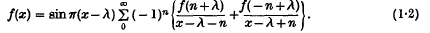
In this note I show that results of Paley- Wiener, Levinson and others on biorthogonal series can be made to yield a consistency theorem for cardinal series based on sequences λn, where

that is, series
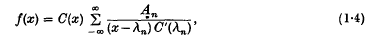
where
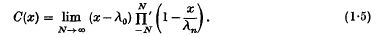
We use Fourier transform technique and need hypotheses, a little more restrictive than Whittaker's, which would reduce in the case 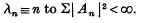 .
.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 50 , Issue 1 , January 1954 , pp. 139 - 142
- Copyright
- Copyright © Cambridge Philosophical Society 1954


