Hostname: page-component-6bf8c574d5-956mj Total loading time: 0 Render date: 2025-02-22T23:26:46.804Z Has data issue: false hasContentIssue false
  • English
  • Français

The connectedness of Sierpiński sponges with rotational and reflectional components and associated graph-directed systems

Part of: Classical measure theory Generalities

Published online by Cambridge University Press:  21 February 2025

HUO-JUN RUAN  and
JIAN-CI XIAO
HUO-JUN RUAN
Affiliation:
Haina Building 2, School of Mathematical Sciences, Zhejiang University, No. 866 Yuhangtang Road, Hangzhou 310058, China. e-mail: [email protected]
JIAN-CI XIAO
Affiliation:
Buiding A17, School of Mathematics, Nanjing University of Aeronautics and Astronautics, No. 29 Jiangjun Road, Nanjing 211106, China. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We provide two methods to characterise the connectedness of all d-dimensional generalised Sierpiński sponges whose corresponding iterated function systems (IFSs) are allowed to have rotational and reflectional components. Our approach is to reduce it to an intersection problem between the coordinates of graph-directed attractors. More precisely, let $(K_1,\ldots,K_n)$ be a Cantor-type graph-directed attractor in 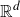${\mathbb {R}}^d$. By creating an auxiliary graph, we provide an effective criterion for whether 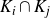$K_i\cap K_j$ is empty for every pair of 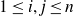$1\leq i,j\leq n$. Moreover, the emptiness can be checked by examining only a finite number of geometric approximations of the attractor. The approach is also applicable to more general graph-directed systems.

MSC classification

Primary: 28A80: Fractals
Secondary: 54A05: Topological spaces and generalizations (closure spaces, etc.)
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , First View , pp. 1 - 24
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Cambridge Philosophical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barański, K.. Hausdorff dimension of the limit sets of some planar geometric constructions. Adv. Math. 210 (2007), 215–245.CrossRefGoogle Scholar
Bonk, M. and Merenkov, S.. Quasisymmetric rigidity of square Sierpiński carpets. Ann. of Math. (2) 177 (2013), 591–643.CrossRefGoogle Scholar
Bonk, M. and Merenkov, S.. Square Sierpiński carpets and Lattès maps. Math. Z. 296 (2020), 695–718.CrossRefGoogle Scholar
Dai, X.-R., Luo, J., Ruan, H.-J., Wang, Y. and Xiao, J.-C.. Connectedness and local cut points of generalized Sierpiński carpets. Asian. J. Math. 27 (2023), 529–570.CrossRefGoogle Scholar
Das, M. and Ngai, S.-M.. Graph-directed iterated function systems with overlaps. Indiana Univ. Math. J. 53 (2004), 109–134.CrossRefGoogle Scholar
Deng, Q.-R. and Lau, K.-S.. Connectedness of a class of planar self-affine tiles. J. Math. Anal. Appl. 380 (2011), 493–500.CrossRefGoogle Scholar
Edgar, G. A. and Golds, J.. A fractal dimension estimate for a graph-directed iterated function system of non-similarities. Indiana Univ. Math. J. 48 (1999), 429–447.CrossRefGoogle Scholar
Edgar, G. A. and Mauldin, R. D.. Multifractal decompositions of digraph recursive fractals. Proc. London Math. Soc. 3 (1992), 604–628.CrossRefGoogle Scholar
Falconer, K. J.. Techniques in Fractal Geometry (John Wiley & Sons, Ltd., Chichester, 1997).Google Scholar
Falconer, K. J. and O’Connor, J.. Symmetry and enumeration of self-similar fractals. Bull. London Math. Soc. 39 (2007), 272–282.CrossRefGoogle Scholar
Farkas, Á.. Dimension approximation of attractors of graph directed IFSs by self-similar sets. Math. Proc. Camb. Phil. Soc. 167 (2019), 193–207.Google Scholar
Fraser, J. M.. On the packing dimension of box-like self-affine sets in the plane. Nonlinearity 25 (2012), 2075–2092.CrossRefGoogle Scholar
Fraser, J. M.. Fractal geometry of Bedford–McMullen carpets. In Pollicot, M. and Vaienti, S., editors, Proceedings of the Fall 2019 Jean-Morlet Chair programme (Springer Lecture Notes Series, 2021).CrossRefGoogle Scholar
Hata, M.. On the structure of self-similar sets. Japan J. Appl. Math. 2 (1985), 381–414.CrossRefGoogle Scholar
Hutchinson, J.. Fractals and self-similarity. Indiana Univ. Math. J. 30 (1981), 713–747.CrossRefGoogle Scholar
Lau, K.-S., Luo, J. J. and Rao, H.. Topological structure of fractal squares. Math. Proc. Camb. Phil. Soc. 155 (2013), 73–86.CrossRefGoogle Scholar
Mauldin, R. D. and Williams, S. C.. Hausdorff dimension in graph directed constructions. Trans. Amer. Math. Soc. 309 (1988), 811–829.CrossRefGoogle Scholar
Olsen, L.. Random geometrically graph directed self-similar multifractals. (Pitman Research Notes in Mathematics Series, vol. 307 (Longman Scientific and Technical, Harlow, 1994).Google Scholar
Olsen, L.. On the Assouad dimension of graph directed Moran fractals. Fractals 19 (2011), 221–226.CrossRefGoogle Scholar
Peitgen, H.-O., Jürgens, H. and Saupe, D.. Chaos and Fractals: New Frontiers of Science (2nd ed., Springer, Berlin, 2004).CrossRefGoogle Scholar
Ruan, H.-J. and Wang, Y.. Topological invariants and Lipschitz equivalence of fractal squares. J. Math. Anal. Appl. 451 (2017), 327–344.CrossRefGoogle Scholar
Shmerkin, P. and Solomyak, B.. Zeros of $\{-1, 0, 1\}$ power series and connectedness loci for self-affine sets. Experiment. Math. 15 (2006), 499–511.CrossRefGoogle Scholar
Solomyak, B.. Connectedness locus for pairs of affine maps and zeros of power series. J. Fractal Geom. 2 (2015), 281–308.CrossRefGoogle Scholar
Strobin, F. and Swaczyna, J.. Connectedness of attractors of a certain family of IFSs. J. Fractal Geom. 7 (2020), 219–231.CrossRefGoogle Scholar
Wang, J.. The open set conditions for graph directed self-similar sets. Random Comput. Dynam. 5 (1997), 283–305.Google Scholar
Wen, Z.-Y. and Xi, L.-F.. On the dimensions of sections for the graph-directed sets. Ann. Acad. Sci. Fenn. Math. 35 (2010), 515–535.CrossRefGoogle Scholar
Xiong, Y. and Xi, L.. Lipschitz equivalence of graph-directed fractals. Studia Math. 194 (2009), 197–205.CrossRefGoogle Scholar
Xi, L.. Differentiable points of Sierpinski-like sponges. Adv. Math. 361 (2020), 106936.CrossRefGoogle Scholar
Xiao, J.-C.. Fractal squares with finitely many connected components. Nonlinearity 34 (2021), 1817–1836.CrossRefGoogle Scholar
Ziegler, G. M.. Lectures on Polytopes (Springer-Verlag, New York, 1995).CrossRefGoogle Scholar