Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-24T02:18:56.444Z Has data issue: false hasContentIssue false
  • English
  • Français

Concerning secondary flow in straight pipes

Published online by Cambridge University Press:  24 October 2008

L. Howarth
L. Howarth
Affiliation:
King's College
Get access Rights & Permissions [Opens in a new window]

Extract

In this paper the condition for the existence of a secondary flow in a straight non-circular pipe is determined according to the modified vorticity transfer theory, with Goldstein's assumed form for the tensor 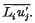It is shown that a secondary motion arises if the mixture length is not constant on the curves along which | grad u | is constant, u being the velocity parallel to the pipe axis.

In problems of turbulent flow treated by means of the modified vorticity transfer theory, the quantity 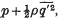where 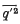is the mean value of the square of the velocity fluctuation and p the mean pressure, plays a part analogous to the pressure in laminar flow. In two-dimensional flow through a channel the theory shows the existence of a gradient of 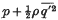across the channel from the central plane to each wall. Qualitative arguments such as are used to explain the existence of a secondary flow for laminar motion in a curved pipe are applied here to show that a secondary flow is to be expected near the short sides in the turbulent flow through a straight rectangular pipe of large length/breadth ratio.

The equations to determine the secondary flow through an almost circular elliptic pipe are discussed, the mixture length being assumed constant on ellipses similar to and concentric with the pipe section. For a first approximation the problem is reduced to the numerical solution of three simultaneous ordinary linear differential equations.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 34 , Issue 3 , July 1938 , pp. 335 - 344
Copyright
Copyright © Cambridge Philosophical Society 1938

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

* See, for example, Taylor, , Proc. Roy. Soc. A, 151 (1935), 495–7.Google Scholar

* Adam's Prize Essay 1934 (unpublished).

† This result was pointed out to me by Prof. Kármán, who obtained it by making assumptions of the same form as those in (5).

* This result is also true when there is a secondary flow.

* Proc. Roy. Soc. A, 155 (1936), 576–96.Google Scholar

† It should be pointed out that the value of was obtained by taking one-third of the maximum found by the ultramicroscope method.

* See, for example, James, Thompson, British Association Report, Dublin 1857, Transactions of the Sections, p. 39.Google Scholar

* Nikuradse, , Ingenieur-Archiv 1 (1930), 306–32.CrossRefGoogle Scholar

† Verhandlungen des 2ten internationalen Kongresses für technische Mechanik (Zürich, 1926), pp. 70–4.Google Scholar

† Dean found a similar result for laminar flow through a curved circular pipe; he found to a first approximation that the viscous stresses arising from the secondary flow balanced those arising from that part of the centrifugal force not balanced by the pressure.

‡ Proc. Roy. Soc. A, 159 (1937), 503.Google Scholar

§ Phil. Mag. 21 (1936), 100.Google Scholar

* Proc. Roy. Soc. A, 145 (1934), 180–211.Google Scholar

* See equation (20) above.

† To the first order in ε both definitions of J lead to the same result.

* ψ is zero at the limits r= 0, a from the boundary conditions.