Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-26T13:34:05.273Z Has data issue: false hasContentIssue false
  • English
  • Français

Computing nilpotent and unipotent canonical forms: a symmetric approach

Published online by Cambridge University Press:  19 October 2011

MATTHEW C. CLARKE
MATTHEW C. CLARKE*
Affiliation:
Trinity College, Cambridge, CB2 1TQ. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let k be an algebraically closed field of any characteristic except 2, and let G = GLn(k) be the general linear group, regarded as an algebraic group over k. Using an algebro-geometric argument and Dynkin–Kostant theory for G we begin by obtaining a canonical form for nilpotent Ad(G)-orbits in 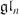(k) which is symmetric with respect to the non-main diagonal (i.e. it is fixed by the map f : (xi,j) ↦ (xn+1−j,n+1−i)), with entries in {0,1}. We then show how to modify this form slightly in order to satisfy a non-degenerate symmetric or skew-symmetric bilinear form, assuming that the orbit does not vanish in the presence of such a form. Replacing G by any simple classical algebraic group we thus obtain a unified approach to computing representatives for nilpotent orbits of all classical Lie algebras. By applying Springer morphisms, this also yields representatives for the corresponding unipotent classes in G. As a corollary we obtain a complete set of generic canonical representatives for the unipotent classes in finite general unitary groups GUn(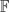q) for all prime powers q.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 152 , Issue 1 , January 2012 , pp. 35 - 53
Copyright
Copyright © Cambridge Philosophical Society 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[Car05]Carter, R. W.Lie Algebras of Finite and Affine Type. Cambridge Studies in Advanced Math. No. 96 (Cambridge University Press, 2005).CrossRefGoogle Scholar
[DG08]De Graaf, W. A.Computing with nilpotent orbits in simple Lie algebras of exceptional type. LMS J. Comput. Math. 11 (2008), 280–297.CrossRefGoogle Scholar
[Ger61]Gerstenhaber, M.Dominance over the classical groups. Ann. of Math. (2) 74 (1961), 532–569.CrossRefGoogle Scholar
[Kaw85]Kawanaka, N. Generalized Gelfand-Graev representations and Ennola duality. In Algebraic Groups and Related Topics. Adv. Stud. Pure Math. vol. 6 (North-Holland, 1985), pp. 179–206.Google Scholar
[Lus05]Lusztig, G.Unipotent elements in small characteristic. Transform. Groups 10 (2005), 449–487.CrossRefGoogle Scholar
[Pop03]Popov, V. L.The cone of Hilbert nullforms. Proc. Steklov Inst. Math. 241 (2003), 177–194, (English translation).Google Scholar
[Sho98]Shoji, T.Shintani descent for special linear groups. J. Algebra 199 (1998), 175–228.CrossRefGoogle Scholar
[SS70]Springer, T. A. and Steinberg, R. Conjugacy classes. In Seminar on Algebraic Groups and Related Finite Groups. Lecture Notes in Math. vol. 131 (Springer, 1970), pp. 167–266.CrossRefGoogle Scholar