Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-24T12:20:10.937Z Has data issue: false hasContentIssue false
  • English
  • Français

The combinatorial structure of the Hughes–Zassenhaus plane of order 25

Published online by Cambridge University Press:  24 October 2008

T. G. Room
T. G. Room
Affiliation:
The Open University, Walton Hall, Bletchley, Buckinghamshire
Get access Rights & Permissions [Opens in a new window]

Abstract

The Hughes–Zassenhaus plane, 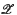, of order 25 is the simplest of the exceptional Hughes planes (see, e.g. (1), p. 391).

In this paper, an incidence table is constructed analogous to tables for the field plane and the regular Hughes plane, and the following rather surprising properties of the plane 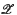emerge:

(i) The table has much greater internal symmetry than either of the analogous tables,

(ii) any polarity with regard to a conic in the central subplane Δ0 of 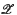extends to two pairs of polarities in 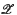one pair with 30 and the other with 60 singular points each in addition to the six in Δ0.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 74 , Issue 2 , September 1973 , pp. 237 - 245
Copyright
Copyright © Cambridge Philosophical Society 1973

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Hall, M.The theory of groups; p. 391 (Macmillan, 1959).Google Scholar
(2)Room, T. G.The combinatorial structure of the Hughes plane. Proc. Cambridge Philos. Soc. 68 (1970), 291–301.Google Scholar
Room, T. G.The combinatorial structure of the Hughes plane. Proc. Cambridge Philos. Soc. 72 (1962), 135–139.CrossRefGoogle Scholar