Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T17:30:07.109Z Has data issue: false hasContentIssue false
  • English
  • Français

Combinatorial proofs of two theorems of Lutz and Stull

Part of: Classical measure theory

Published online by Cambridge University Press:  15 February 2021

TUOMAS ORPONEN
TUOMAS ORPONEN*
Affiliation:
Department of Mathematics and Statistics, University of Jyväskylä P.O. Box 35 (Mattilanniemi MaD) FI-40014University of Jyväskylä, Finland e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Recently, Lutz and Stull used methods from algorithmic information theory to prove two new Marstrand-type projection theorems, concerning subsets of Euclidean space which are not assumed to be Borel, or even analytic. One of the theorems states that if 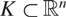\[K \subset {\mathbb{R}^n}\] is any set with equal Hausdorff and packing dimensions, then

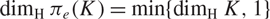\begin{equation} \[{\dim _{\text{H}}}{\pi _e}(K) = \min \{ {\dim _{\text{H}}}{\text{ }}K{\text{, 1}}\} \] \end{equation}

for almost every 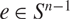\[e \in {S^{n - 1}}\]. Here 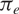\[{\pi _e}\] stands for orthogonal projection to span (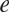\[e\]). The primary purpose of this paper is to present proofs for Lutz and Stull’s projection theorems which do not refer to information theoretic concepts. Instead, they will rely on combinatorial-geometric arguments, such as discretised versions of Kaufman’s “potential theoretic” method, the pigeonhole principle, and a lemma of Katz and Tao. A secondary purpose is to generalise Lutz and Stull’s theorems: the versions in this paper apply to orthogonal projections to m-planes in 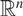\[{\mathbb{R}^n}\], for all 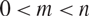\[0 < m < n\].

MSC classification

Primary: 28A80: Fractals
Secondary: 28A78: Hausdorff and packing measures
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 171 , Issue 3 , November 2021 , pp. 503 - 514
Copyright
© Cambridge Philosophical Society 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Davies, R. O.. Two counterexamples concerning Hausdorff dimensions of projections. Colloq. Math. 42 (1979), 53–58.CrossRefGoogle Scholar
Falconer, K. J. and Howroyd, J. D.. Projection theorems for box and packing dimensions. Math. Proc. Camb. Phil. Soc. 119(2) (1996), 287–295.CrossRefGoogle Scholar
Falconer, K.. Fractal Geometry. Mathematical foundations and applications. (John Wiley & Sons, Ltd., Chichester, third edition, 2014).Google Scholar
Falconer, K. J.. A capacity approach to box and packing dimensions of projections of sets and exceptional directions. J. Fractal Geom. (to appear) (2020).CrossRefGoogle Scholar
Fässler, K. and Orponen, T.. On restricted families of projections in \[{\mathbb{R}^3}\]. Proc. Lond. Math. Soc. 3 109(2) (2014), 353–381.CrossRefGoogle Scholar
Järvenpää, M.. On the upper Minkowski dimension, the packing dimension, and orthogonal projections. Ann. Acad. Sci. Fenn. Ser. A I Math. Dissertationes (99) (1994), 34.Google Scholar
Katz, N. H. and Tao, T.. Some connections between Falconer’s distance set conjecture and sets of Furstenburg type. New York J. Math. 7 (2001), 149–187.Google Scholar
Kaufman, R.. On Hausdorff dimension of projections. Mathematika 15 (1968), 153–155.CrossRefGoogle Scholar
Lutz, J. H. and Lutz, N.. Algorithmic information, plane Kakeya sets and conditional dimension. ACM Trans. Comput. Theory 10(2) (2018), Art. 7, 22.CrossRefGoogle Scholar
Lutz, N. and Stull, D. M.. Projection theorems using effective dimension. In 43 rd International Symposium on Mathematical Foundations of Computer Science, volume 117 of LIPIcs. Leibniz Int. Proc. Inform., pages Art. No. 71, 15. Schloss Dagstuhl. Leibniz-Zent. Inform., Wadern, (2018). Also available at arXiv:1711.02124.Google Scholar
Marstrand, J. M.. Some fundamental geometrical properties of plane sets of fractional dimensions. Proc. London Math. Soc. (3) 4 (1954), 257–302.CrossRefGoogle Scholar
Mattila, P.. Geometry of Sets and Measures in Euclidean Spaces. Fractals and Rectifiability. (Cambridge University Press, 1st paperback ed. edition, 1999).Google Scholar
Mattila, P.. Hausdorff dimension, orthogonal projections and intersections with planes. Ann. Acad. Sci. Fenn. Ser. A I Math. 1(2) (1975), 227–244.CrossRefGoogle Scholar
Orponen, T.. On the packing dimension and category of exceptional sets of orthogonal projections. Ann. Mat. Pura Appl. (4) 194(3) (2015), 843–880.CrossRefGoogle Scholar