Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-25T01:08:44.332Z Has data issue: false hasContentIssue false
  • English
  • Français

Cohomology operations and duality

Published online by Cambridge University Press:  24 October 2008

C. R. F. Maunder
C. R. F. Maunder
Affiliation:
Christ's College, Cambridge
Get access Rights & Permissions [Opens in a new window]

Extract

Since Thom first introduced the notion of the ‘dual’ of a Steenrod square, in (12), it has become apparent that calculation with such duals in the cohomology of, say, a simplicial complex X will often yield information about the impossibility of embedding X in Sn, for certain values of n. For example, the celebrated theorem that 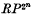cannot be embedded in 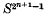can easily be proved in this way. In this paper, we seek to generalize this method to any pair of extraordinary cohomology theories h* and k*, and natural stable cohomology operation θ: h* → k*. We show in section 3 that a simplicial embeddingf: X → Sn gives rise via the Alexander duality isomorphism to a homology operation

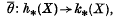
which is independent of n, the particular embedding f, and even the particular triangulations of X and Sn. If h* and k* are multiplicative cohomology theories, there are Kronecker products

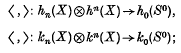
if h0(S0) = k0(S0) = G, a field, and the Kronecker products make h*, h* and k*, k* into dual vector spaces over G, then 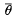can be turned into a cohomology operation c(θ): k*(X)→h*(X), by using this duality. This is certainly true if h* = k* = H*(;Zp), p prime, and in this case we have the original situation considered by Thom, who showed, for example, that

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 64 , Issue 1 , January 1968 , pp. 15 - 30
Copyright
Copyright © Cambridge Philosophical Society 1968

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Adams, J. F.Vector fields on spheres. Ann. of Math. 75 (1962), 603–632.CrossRefGoogle Scholar
(2)Araki, S. and Toda, H.Multiplicative structures in mod q cohomology theories. I. Osaka J. Math. 2 (1965), 71–115.Google Scholar
(3)Araki, S. and Toda, H.Multiplicative structures in mod q cohomology theories. II. Osaka J. Math. 3 (1966), 81–120.Google Scholar
(4)Atiyah, M. F. and Hirzebruch, F. Vector bundles and homogeneous spaces. Proceedings of Symposia in Pure Mathematics, vol. III, pp. 7–38. (American Mathematical Society, Providence, R.I., 1960.)Google Scholar
(5)Brown, E. H.Cohomology theories. Ann. of Math. 75 (1962), 467–484.CrossRefGoogle Scholar
(6)Dold, A.Half-exact functors (Mimeographed notes, Seattle, 1963).Google Scholar
(7)Eilenberg, S. and Steenrod, N.Foundations of algebraic topology (Princeton, 1952).CrossRefGoogle Scholar
(8)Maunder, C. R. F.Stable operations in mod p K-theory. Proc. Cambridge Philos. Soc. 63 (1967), 631–646.CrossRefGoogle Scholar
(9)Maunder, C. R. F.Mod p cohomology theories and the Bockstein spectral sequence. Proc. Cambridge Philos. Soc. 63 (1967), 23–43.CrossRefGoogle Scholar
(10)Puppe, D.Homotopiemengen und ihre induzierten Abbildungen. I. Math. Z. 69 (1958), 199–244.Google Scholar
(11)Spanier, E. H. and Whitehead, J. H. C.Duality in homotopy theory. Mathematika 2 (1955), 56–80.CrossRefGoogle Scholar
(12)Thom, R.Espaces fibrés en sphères et carrés de Steenrod. Ann. Sci. École Norm. Sup. (3), 69 (1952), 109–182.CrossRefGoogle Scholar
(13)Whitehead, G. W.Generalized homology theories. Trans. Amer. Math. Soc. 102 (1962), 227–283.CrossRefGoogle Scholar