Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-25T02:49:24.293Z Has data issue: false hasContentIssue false
  • English
  • Français

A characterization of M-Summands

Published online by Cambridge University Press:  24 October 2008

Richard Evans
Richard Evans
Affiliation:
Freie Universität, Berlin
Get access Rights & Permissions [Opens in a new window]

Extract

In the structure theory of Banach spaces as developed in (1), an important role is played by subspaces which are the ranges of projections having norm properties akin to those of the classical Banach spaces. A linear projection e on a Banach space V is called an M-projection if

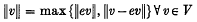
and an L-projection if, instead

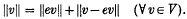
A closed subspace J of V is called an M-Summand if it is the range of an M-projection and an M-Ideal if J0 is the range of an L-projection in V′. Every M-Summand is an M-Ideal but the reverse is false.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 76 , Issue 1 , July 1974 , pp. 157 - 159
Copyright
Copyright © Cambridge Philosophical Society 1974

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Alfsen, E. M. and Effros, E.Structure in real Banach spaces. Parts I and II. Ann. of Math. 96 (1972), 98–173.CrossRefGoogle Scholar