No CrossRef data available.
Article contents
A centred norm inequality for singular integral operators
Published online by Cambridge University Press: 24 October 2008
Abstract
Let K be a standard singular integral kernel on ℝ satisfying the usual Hölder continuity condition of order δ, and define 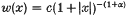 (where c is chosen so that the integral of w is 1),
(where c is chosen so that the integral of w is 1), 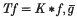 the mean of g with respect to the measure w(x) dx, and ‖·‖p the Lp norm with respect to w(x) dx. Although the inequality
the mean of g with respect to the measure w(x) dx, and ‖·‖p the Lp norm with respect to w(x) dx. Although the inequality 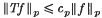 is not true in general, the centred norm inequality
is not true in general, the centred norm inequality 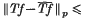
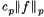 does hold for 1 < p < ∞ if α < δ.
does hold for 1 < p < ∞ if α < δ.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 112 , Issue 2 , September 1992 , pp. 369 - 383
- Copyright
- Copyright © Cambridge Philosophical Society 1992
References
REFERENCES
[1]Bass, R. F.. A probabilistic approach to the boundedness of singular integral operators. In Séminaire de Probabilités XXIV, Lecture Notes in Math. vol. 1426 (Springer-Verlag, 1990), pp. 15–40.Google Scholar
[2]Fefferman, C. and Stein, E. M.. Hp spaces of several variables. Acta Math. 129 (1972), 137–193.CrossRefGoogle Scholar
[3]Stein, E. M.. Singular Integrals and Differentiability Properties of Functions (Princeton University Press, 1970).Google Scholar


