Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-24T16:44:45.203Z Has data issue: false hasContentIssue false
  • English
  • Français

Canonical systems on a reducible variety

Published online by Cambridge University Press:  24 October 2008

R. E. Macpherson
R. E. Macpherson
Affiliation:
King's CollegeCambridge
Get access Rights & Permissions [Opens in a new window]

Extract

The object of this note is to extend the proof, for the general canonical varieties of any dimension k < d on a Vd whose existence was established by Dr Todd in a recent paper, of the property of adjunction given by the relation

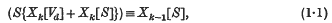
where S is any non-singular variety of dimension d−1 lying on Vd, and Xk[S] denotes the canonical system of dimension k on S. This formula was proved by Todd in the case when Vd is a general non-singular variety, and S is non-singular and belongs to a sufficiently general linear system. Using this result, I show how to remove the latter restriction. (1·1) cannot be taken, without further proof, as defining canonical systems on virtual or isolated varieties, as is done by B. Segre, since the canonical systems on an effective isolated variety are already well defined.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 35 , Issue 3 , July 1939 , pp. 389 - 393
Copyright
Copyright © Cambridge Philosophical Society 1939

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

* Todd, J. A., Proc. London Math. Soc. (2) 43 (1937), 127–38.Google Scholar All the results quoted will be found in this paper. See also a paper by J. A. Todd in course of publication in Proc. London Math. Soc.

† Segre, B., Mem. R. Accad. Ital. 5 (1933–1934), 512.Google Scholar

‡ Roth, L., Proc. Cambridge Phil. Soc. 29 (1933), 88–94.CrossRefGoogle Scholar

* L. Roth, loc. cit.

† J. A. Todd, loc. cit.

* J. A. Todd, loc. cit.