Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-24T16:27:46.940Z Has data issue: false hasContentIssue false
  • English
  • Français

Bounded representations of the positive values of an indefinite quadratic form

Published online by Cambridge University Press:  24 October 2008

B. Lawton
B. Lawton
Affiliation:
Bedford CollegeLondon, N.W.1
Get access Rights & Permissions [Opens in a new window]

Extract

Let

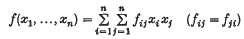
be a real quadratic form in n variables (n ≥ 2) with integral coefficients and determinant D = |fij| ≠ 0. Cassels ((1),(2)) has recently proved that if the equation f = 0 is properly soluble in integers x1, …, xn, then there is a solution satisfying

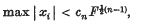
where F = max | fij and cn depends only on n. An example given by Kneser (see (2)) shows that the exponent ½(n – 1) is best possible. A simpler proof of Cassels's result has since been given by Davenport(3), and the theorem has been improved in certain cases by Watson(4). Here I consider the inequality f(x1, …, xn) > 0, where f is an indefinite form, and obtain a result analogous to that of Cassels.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 54 , Issue 1 , January 1958 , pp. 14 - 17
Copyright
Copyright © Cambridge Philosophical Society 1958

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Cassels, J. W. S.Proc. Camb. Phil. Soc. 51 (1955), 262–4.CrossRefGoogle Scholar
(2)Cassels, J. W. S.Proc. Camb. Phil. Soc. 52 (1956), 604.CrossRefGoogle Scholar
(3)Davenport, H.Proc. Camb. Phil. Soc. 53 (1957), 539–40.CrossRefGoogle Scholar
(4)Watson, G. L.Proc. Camb. Phil. Soc. 53 (1957), 541–3.CrossRefGoogle Scholar
(5)Mirsky, L.Introduction to linear algebra (Oxford, 1955).Google Scholar