Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-27T18:45:24.803Z Has data issue: false hasContentIssue false
  • English
  • Français

Best L∞-approximation of measurable, vector-valued functions

Published online by Cambridge University Press:  24 October 2008

Abdallah M. Al-Rashed  and
Richard B. Darst
Abdallah M. Al-Rashed
Affiliation:
Department of Mathematics, King Saud University, Riyadh, Saudi Arabia
Richard B. Darst
Affiliation:
Department of Mathematics, Colorado State University, Fort Collins, Colorado, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Abstract

Let (Ω, 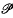,μ) be a probability space, and let 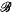be a sub-sigma-algebra of 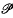. Let X be a uniformly convex Banach space. Let A =L∞(Ω, 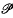, μ X) denote the Banach space of (equivalence classes of) essentially bounded μ-Bochner integrable functions g: Ω.→ X, normed by the function ∥.∥∞ defined for g ∈ A by

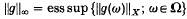
(cf. [6] for a discussion of this space). Let B = L∞(Ω, , μ X), and let f ε A. A sufficient condition for g ε B to be a best L∞-approximation to f by elements of B is established herein.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 96 , Issue 3 , November 1984 , pp. 477 - 481
Copyright
Copyright © Cambridge Philosophical Society 1984

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Al-Rashbd, A. M.. Best L ∞-approximation in probability spaces. J. Math. Anal. Appl. 91 (1983), 1–8.Google Scholar
[1]Al-Rashed, A. M. and Dabst, R. B.. Convergence of best best L ∞-approximations. Proc. Amer. Math. Soc. 83 (1981), 690–692.Google Scholar
[1]Darst, R. B.. Convergence of Lp-approximation as p → ∞. Proc. Amer. Math. Soc. 81 (1981), 433–436.Google Scholar
[1]Dabst, R. B.. Approximation in Lp-approximation 1 < p < ∞.Measure Theory and Its Applications, ed. Golden, G. A. and Wheeler, R. F. (Northern Illinois University, DeKalb, Illinois 1981), pp. 193–199.Google Scholar
[1]Darst, R. B., Legg, D. A. and Townsend, D. W.. The Polya algorithm in L ∞-approximations. J. Approx. Theory 38 (1983), 209–220.Google Scholar
[1]Diestel, J. and Uhl, J. R.. Vector Measures. Math. Surveys 15 (American Mathematical Society, 1977).Google Scholar
[1]Holmes, R. B.. A Course on Optimization and Best Approximation. Lecture Notes in Math., vol. 257 (Springer-Verlag, 1972).CrossRefGoogle Scholar