Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-25T04:48:51.562Z Has data issue: false hasContentIssue false
  • English
  • Français

Bending of Curvilinear and Rectilinear Polygonal Plates Symmetrically Loaded Over a Concentric Circle

Published online by Cambridge University Press:  24 October 2008

W. A. Bassali  and
N. O. M. Hanna
W. A. Bassali
Affiliation:
Faculty of Science University of AlexandriaAlexandria, Egypt
N. O. M. Hanna
Affiliation:
Faculty of Engineering Ain Shams UniversityCairo, Egypt
Get access Rights & Permissions [Opens in a new window]

Abstract

Complex variable methods are applied to obtain exact solutions for the complex potentials and deflexions of thin isotropic slabs bounded by regular curvilinear polygonal contours with n sides and subject to symmetrical loading distributed over a concentric circle. The supported boundary is either clamped or has equal boundary cross-couples. The plates taken in the z-plane are conformally mapped on the unit circle in the ζ-plane by the mapping function 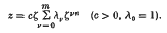. Polynomial approximations to the Schwarz—Christoffel transformations are then used to discuss the bending of clamped and simply supported rectilinear plates symmetrically loaded over a concentric circle or acted upon by a central point load.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 57 , Issue 1 , January 1961 , pp. 166 - 179
Copyright
Copyright © Cambridge Philosophical Society 1961

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Bassali, W. A., Proc. Camb. Phil. Soc. 52 (1956), 734–49.CrossRefGoogle Scholar
(2)Bassali, W. A., Bull. Fac. Sci. Alexandria, 2 (1958), 3.Google Scholar
(3)Bassali, W. A., Proc. Camb. Phil. Soc. 55 (1959), 110.Google Scholar
(4)Bassali, W. A., J. Mech. Phys. Solids, 7 (1959), 145.CrossRefGoogle Scholar
(5)Bassali, W. A., Z. angew. Math. Mech. 40 (1960).Google Scholar
(6)Bassali, W. A., and Dawoud, R. H., Proc. Camb. Phil. Soc. 52 (1956), 584.Google Scholar
(7)Bassali, W. A., and Dawoud, R. H., Proc. Math. Phys. Soc. Egypt, 21 (1957), 1.Google Scholar
(8)Bassali, W. A., and Nassit, M., Proc. Camb. Phil. Soc. 55 (1959), 101.CrossRefGoogle Scholar
(9)Bromwich, T. J. I'A., An introduction to the theory of infinite series (London, 1926).Google Scholar
(10)Deverall, L. I., J. Appl. Mech. 24 (1957), 295.CrossRefGoogle Scholar
(11)Halivov, Z. I., Amer. Math. Soc. (Russian translation), 87 (1953), 5.Google Scholar
(12)Muskhelishvili, N. I., Some basic problems of the mathematical theory of elasticity, 3rd ed. (Moscow, 1949).Google Scholar
(13)Oberhettinger, F., and Magnus, W., Anwendung der Elliptischen Funktionen in Physik und Technik (Berlin, 1949).Google Scholar
(14)Sapondzyan, O. M., Akad. Nauk Armyan. SSR Izv. Fiz.-Mat. Estest. Tekh. Nauki, 7 (1954), 19–43.Google Scholar
(15)Sapondzyan, O. M., Akad. Nauk Armyan. SSR Izv. Fiz.-Mat. Estest. Tekh. Nauki, 9 (1956), 61–75.Google Scholar
(16)Seth, B. R., Phil. Mag. 38 (1947), 282.CrossRefGoogle Scholar
(17)Sokolnikoff, I. S., Mathematical theory of elasticity, 2nd ed. (New York, 1956).Google Scholar
(18)Stevenson, A. C., Phil. Mag. 34 (1943), 105.Google Scholar
(19)Timoshenko, S., Theory of plates and shells (New York, 1940).Google Scholar
(20)Tiffen, R., Quart. J. Mech. Appl. Math. 8 (1955), 237.CrossRefGoogle Scholar
(21)Winslow, A. M., Quart. J. Mech. Appl. Math. 10 (1957), 160.CrossRefGoogle Scholar