Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T01:17:12.614Z Has data issue: false hasContentIssue false
  • English
  • Français

Banach spaces whose algebras of operators have a large group of unitary elements

Published online by Cambridge University Press:  01 January 2008

JULIO BECERRA GUERRERO ,
MARÍA BURGOS ,
EL AMIN KAIDI  and
ÁNGEL RODRÍGUEZ PALACIOS
JULIO BECERRA GUERRERO
Affiliation:
Departamento de Matemática Aplicada, Universidad de Granada, Facultad de Ciencias, 18071-Granada, Spain. e-mail: [email protected]
MARÍA BURGOS
Affiliation:
Departamento de Álgebra y Análisis Matemático, Universidad de Almería, Facultad de Ciencias Experimentales, 04120-Almería, Spain. e-mail: [email protected]; [email protected]
EL AMIN KAIDI
Affiliation:
Departamento de Álgebra y Análisis Matemático, Universidad de Almería, Facultad de Ciencias Experimentales, 04120-Almería, Spain. e-mail: [email protected]; [email protected]
ÁNGEL RODRÍGUEZ PALACIOS
Affiliation:
Departamento de Álgebra y Análisis Matemático, Universidad de Almería, Facultad de Ciencias Experimentales, 04120-Almería, Spain. e-mail: [email protected]; [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that a complex Banach space X is a Hilbert space if (and only if) the Banach algebra 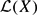(of all bounded linear operator on X) is unitary and there exists a conjugate-linear algebra involution • on 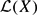satisfying T• = T−1 for every surjective linear isometry T on X. Appropriate variants for real spaces of the result just quoted are also proven. Moreover, we show that a real Banach space X is a Hilbert space if and only if it is a real JB*-triple and 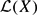is -unitary, where stands for the dual weak-operator topology.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 144 , Issue 1 , January 2008 , pp. 97 - 108
Copyright
Copyright © Cambridge Philosophical Society 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Becerra, J., Burgos, M., Kaidi, A. and Rodr'iguez, A.. Banach algebras with large groups of unitary elements. Quart. J. Math 58 (2007) 203–220.Google Scholar
[2]Becerra, J., Cowell, S., Rodr'iguez, A. and Wood, G. V.. Unitary Banach algebras. Studia Math 162 (2004), 25–51.Google Scholar
[3]Becerra, J., L'opez, G., Peralta, A. M. and Rodr'iguez, A.. Relatively weakly open sets in closed balls of Banach spaces, and real JB*-triples of finite rank. Math. Ann 330 (2004), 45–58.Google Scholar
[4]Becerra, J. and Martín, M.. The Daugavet property of C*-algebras, JB*-triples, and of their isometric preduals. J. Funct. Anal 224 (2005), 316–337.CrossRefGoogle Scholar
[5]Becerra, J. and Rodriguez, A.. The geometry of convex transitive Banach spaces. Bull. London Math. Soc. 31 (1999), 323–331.CrossRefGoogle Scholar
[6]Becerra, J. and Rodriguez, A.. Transistivity of the norm on Banach spaces having a Jordan structure. Manuscripta Math 102 (2000), 111–127.CrossRefGoogle Scholar
[7]Becerra, J., Rodriguez, A. and Wood, G.. Banach spaces whose algebras of operators are unitary: a holomorphic approach. Bull. London Math. Soc 35 (2003), 218–224.Google Scholar
[8]Bonsall, F. F. and Duncan, J.. Complete Normed Algebras (Springer-Verlag, 1973).CrossRefGoogle Scholar
[9]Cowie, E. R.. Isometries in Banach algebras. Ph. D. thesis. Swansea (1981).Google Scholar
[10]Cowie, E. R.. An analytic characterization of groups with no finite conjugacy classes. Proc. Amer. Math. Soc 87 (1983), 7–10.CrossRefGoogle Scholar
[11]Foias, C.. Sur certains theoremes de J. von Neumann concernant les ensembles spectraux. Acta Sci. Math 18 (1957), 15–20.Google Scholar
[12]Hansen, M. L. and Kadison, R. V.. Banach algebras with unitary norms. Pacific J. Math 175 (1996), 535–552.CrossRefGoogle Scholar
[13]Isidro, J. M., Kaup, W. and Rodríguez, A.. On real forms of JB*-triples. Manuscripta Math 86 (1995), 311–335.CrossRefGoogle Scholar
[14]Jacobson, N.. Structure of rings. Amer. Math. Soc. Coll. Publ. 37 (Providence, Rhode Island 1968).Google Scholar
[15]Kakutani, S. and Mackey, G. W.. Two characterizations of real Hilbert space. Ann. of Math 45 (1944), 50–58.CrossRefGoogle Scholar
[16]Kalton, N. J.. Spaces of compact operators. Math. Ann 208 (1974), 267–278.CrossRefGoogle Scholar
[17]Kaup, W.. Über die Automorphismen Grasmannerscher Mannigfaltigkeiten unendlicher Dimension. Math. Z 144 (1975), 75–96.CrossRefGoogle Scholar
[18]Kaup, W.. A Riemann mapping theorem for bounded symmetric domains in complex Banach spaces. Math. Z 183 (1983), 503–529.CrossRefGoogle Scholar
[19]Martìnez, J. and Peralta, A. M.. Separate weak*-continuity of the triple product in dual real JB*-triples. Math. Z 234, 635–646.CrossRefGoogle Scholar
[20]Navarro, M. A.. Some characterizations of finite-dimensional Hilbert spaces. J. Math. Anal. Appl 223 (1998), 364–365.CrossRefGoogle Scholar
[21]Peralta, A. M. and Stach'o, L. L.. Atomic decomposition of real JBW*-triples. Quart. J. Math 52 (2001), 79–87.CrossRefGoogle Scholar
[22]Rickart, C. E.. General Theory of Banach Algebras (Kreiger, 1974).Google Scholar
[23]Rodrìguez, A.. Absolute valued algebras of degree two. In Nonassociative Algebra and its applications (Ed. S. González), 350–356 (Kluwer Academic Publishers, 1994).Google Scholar
[24]Rolewicz, S.. Metric Linear Spaces (Reidel, 1985).Google Scholar
[25]Wood, G. V.. Maximal algebra norms. Contemp. Math 321 (2003), 335–345.CrossRefGoogle Scholar