Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-28T10:39:21.728Z Has data issue: false hasContentIssue false
  • English
  • Français

Banach algebras whose duals consist of multipliers

Published online by Cambridge University Press:  24 October 2008

E. O. Oshobi  and
J. S. Pym
E. O. Oshobi
Affiliation:
Department of Mathematics, University of Ife, Ile-Ife, Nigeria
J. S. Pym
Affiliation:
Department of Pure Mathematics, University of Sheffield, Sheffield S10 2TN
Get access Rights & Permissions [Opens in a new window]

Extract

A few years ago, the authors considered briefly Banach algebras whose duals could be identified ‘naturally’ with their multiplier algebras [17]. In this context, naturalness can be interpreted as meaning that, for each element b of the algebra B and each pair of elements u, v of the dual B′,

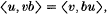
where 〈, 〉 denotes the dual pairing and the products are of elements of B′ regarded as left or right multipliers on B. In the present paper we return to the same circle of ideas but begin with a more general situation. We assume only that the algebra B is injectively embedded in its algebra of left, and in its algebra of right, multipliers and that its dual B′ can be injectively embedded in the algebra M(B) of double multipliers on B (definition below) in such a way that the above relation holds. From these assumptions we shall prove that there is a normed algebra A such that M(B) is the dual of A and is the algebra of continuous left multipliers on A (or, equally, right multipliers).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 102 , Issue 3 , November 1987 , pp. 481 - 505
Copyright
Copyright © Cambridge Philosophical Society 1987

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Arens, R.. Operations induced in function classes. Monatsh. Math. 55 (1951), 1–19.CrossRefGoogle Scholar
[2]Arens, R.. The adjoint of a bilinear operation. Proc. Amer. Math. Soc. 2 (1951), 839–848.CrossRefGoogle Scholar
[3]Bonsall, F. F. and Duncan, J.. Complete normed algebras (Springer-Verlag, 1973).CrossRefGoogle Scholar
[4]Cigler, J., Losert, V. and Michor, P.. Banach modules and functors on categories of Banach spaces (Dekker, 1979).Google Scholar
[5]Civin, P. and Yood, B.. The second conjugate space of a Banach algebra as an algebra. Pacific J. Math. 11 (1961), 847–870.CrossRefGoogle Scholar
[6]Diestel, J. and Uhl, J. J.. Vector measures. Mathematical Surveys 15 (Amer. Math. Soc, 1977).CrossRefGoogle Scholar
[7]Duncan, J. and Hosseniun, S. A. R.. The second dual of a Banach algebra. Proc. Roy. Soc. Edinburgh A, 84 (1979), 309–325.CrossRefGoogle Scholar
[8]Dunford, N. and Schwartz, J. T.. Linear operators (Wiley, Vol. I, 1958; Vol. II, 1963).Google Scholar
[9]Dunkl, C. F. and Ramirez, D. E.. Weakly almost periodic functionals on the Fourier algebra. Trans. Amer. Math. Soc. 185 (1973), 501–514.CrossRefGoogle Scholar
[10]Figa-Talamanca., A.Translation invariant operators in Lp. Duke Math. J. 32 (1965), 495–501.CrossRefGoogle Scholar
[11]Gohberg, I. C. and Krein, M. G.. Introduction to the theory of linear nonselfadjoint operators (Nauka, 1965) Russian; (Amer. Math. Soc. Translations 18, 1968) English translation.Google Scholar
[12]Grosser, M.. Bidualräume und Vervollständigungen von Banachmoduln. Lecture Notes in Math. 717 (Springer-Verlag, 1979).CrossRefGoogle Scholar
[13]Grothendieck, A.. Produits tensoriels topologiques et espaces nucléaires (Memoirs Amer. Math. Soc. 16, 1955).CrossRefGoogle Scholar
[14]Hewitt, E. and Ross, K. A.. Abstract harmonic analysis 1 (Springer-Verlag, 1963).Google Scholar
[15]Johnson, B. E.. An introduction to the theory of centralizers. Proc. London Math. Soc. 14 (1964), 299–320.CrossRefGoogle Scholar
[16]Larsen, R.. An introduction to the theory of multipliers (Springer-Verlag, 1971).CrossRefGoogle Scholar
[17]Oshobi, E. O. and Pym, J. S.. Banach algebras whose duals are multiplier algebras. Bull. London Math. Soc. 13 (1981), 66–68.CrossRefGoogle Scholar
[18]Palmer, T. W.. The bidual of the compact operators. Trans. Amer. Math. Soc. 288 (1985), 827–840.CrossRefGoogle Scholar
[19]Pym, J. S.. The convolution of functionals on spaces of bounded functions. Proc. London Math. Soc. 15 (1965), 84–104.Google Scholar
[20]Ringrose, J. R.. Compact non-self-adjoint operators (Van Nostrand, 1971).Google Scholar
[21]Tomiuk, B. J.. Arens regularity and the algebra of double multipliers. Proc. Amer. Math. Soc. 81 (1981), 293–298.CrossRefGoogle Scholar
[22]Ülger, A.. Continuity of weakly almost periodic functionals on L 1(G). Quart. J. Math. (Oxford) 37 (1986), 495–497.CrossRefGoogle Scholar
[23]Young, N. J.. The irregularity of multiplication in group algebras. Quart. J. Math. (Oxford) 24 (1973), 59–62.CrossRefGoogle Scholar
[24]Young, N. J.. Periodicity of functionals and representations of normed algebras on reflexive spaces. Proc. Edinburgh Math. Soc. 20 (1976), 99–120.CrossRefGoogle Scholar