Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Carne, T. K.
1979.
Not all H′-algebras are operator algebras.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 86,
Issue. 2,
p.
243.
Tonge, Andrew M.
1986.
Bilinear mappings and trace class ideals.
Mathematische Annalen,
Vol. 275,
Issue. 2,
p.
281.
Muller, M. A.
1987.
QUOTIENTS OF 2-SUMMING ALGEBRAS.
Quaestiones Mathematicae,
Vol. 10,
Issue. 4,
p.
367.
Iochum, B.
and
Loupias, G.
1989.
Arens regularity and local reflexivity principle for Banach algebras.
Mathematische Annalen,
Vol. 284,
Issue. 1,
p.
23.
Blecher, David P.
1990.
Tensor products which do not preserve operator algebras.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 108,
Issue. 2,
p.
395.
Blecher, David P.
1990.
Commutativity in operator algebras.
Proceedings of the American Mathematical Society,
Vol. 109,
Issue. 3,
p.
709.
Blecher, David P.
1995.
A completely bounded characterization of operator algebras.
Mathematische Annalen,
Vol. 303,
Issue. 1,
p.
227.
Blecher, David P.
2001.
The Shilov Boundary of an Operator Space and the Characterization Theorems.
Journal of Functional Analysis,
Vol. 182,
Issue. 2,
p.
280.


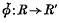 by
by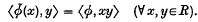
 be
be 