Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-25T04:24:24.586Z Has data issue: false hasContentIssue false
  • English
  • Français

Augmentation quotients of some nonabelian finite groups

Published online by Cambridge University Press:  24 October 2008

Gerald Losey  and
Nora Losey
Gerald Losey
Affiliation:
University of Manitoba, Winnipeg, Canada
Nora Losey
Affiliation:
University of Manitoba, Winnipeg, Canada
Get access Rights & Permissions [Opens in a new window]

Extract

1. Let G be a group, ZG its integral group ring and Δ = ΔG the augmentation ideal ZG By an augmentation quotient of G we mean any one of the ZG-modules

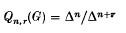
where n, r ≥ 1. In recent years there has been a great deal of interest in determining the abelian group structure of the augmentation quotients Qn(G) = Qn,1(G) and

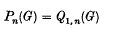
(see (1, 2, 7, 8, 9, 12, 13, 14, 15)). Passi(8) has shown that in order to determine Qn(G) and Pn(G) for finite G it is sufficient to assume that G is a p-group. Passi(8, 9) and Singer(13, 14) have obtained information on the structure of these quotients for certain classes of abelian p-groups. However little seems to be known of a quantitative nature for nonabelian groups. In (2) Bachmann and Grünenfelder have proved the following qualitative result: if G is a finite group then there exist natural numbers n0 and π such that Qn(G) ≅ Qn+π (G) for all n ≥ n0; if Gω is the nilpotent residual of G and G/Gω has class c then π divides l.c.m. {1, 2, …, c}. There do not appear to be any examples in the literature of this periodic behaviour for c > 1. One of goals here is to present such examples. These examples will be from the class of finite p-groups in which the lower central series is an Np-series.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 85 , Issue 2 , March 1979 , pp. 261 - 270
Copyright
Copyright © Cambridge Philosophical Society 1979

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Bachmann, F. and Grünenfelder, L.Homological methods and the third dimension subgroup. Comm. Math. Helv. 47 (1972), 526–531.Google Scholar
(2)Bachmann, F. and Grünenfelder, L.The periodicity in the graded ring associated with an integral group ring. J. Pure and Applied Algebra 5 (1974), 253–264.CrossRefGoogle Scholar
(3)Curtis, E. B.Simplicial homotopy theory. Advances in Math. 6 (1971), 107–209.CrossRefGoogle Scholar
(4)Jennings, S. A.The structure of the group ring of a p-group over a modular field. Trans. Amer. Math. Soc. 50 (1941), 175–185.Google Scholar
(5)Lazard, M.Sur les groupes nilpotentes et les anneaux de Lie. Ann. Sci. Ecole Norm. Sup. (3) 71 (1954), 101–190.CrossRefGoogle Scholar
(6)Losey, G.N-series and filtrations of the augmentation ideal. Canad. J. Math. 26 (1974), 962–977.CrossRefGoogle Scholar
(7)Losey, G.On the structure of Q 2(G) of finitely generated groups. Canad. J. Math. 25 (1973), 353–359.CrossRefGoogle Scholar
(8)Passi, I. B. S.Polynomial maps on groups. J. Algebra 9 (1968), 121–151.Google Scholar
(9)Passi, I. B. S.Polynomial functors. Proc. Cambridge Philos. Soc. 66 (1969), 505–512.CrossRefGoogle Scholar
(10)Passman, D. S.Algebraic Theory of Group Rings. New York, 1977.Google Scholar
(11)Quillen, D. G.On the associated graded ring of a group ring. J. Algebra 10 (1968), 411–418.Google Scholar
(12)Schmidt, B. K. Mappings of degree n from groups to abelian groups. Doctoral dissertation, Princeton University, 1972.Google Scholar
(13)Singer, M.Determination of the augmentation terminal for all abelian groups of exponent 8. Comm. Algebra 5 (1977), 87–100.Google Scholar
(14)Singer, M.On the augmentation terminal of a finite abelian group. J. Algebra 41 (1966), 196–201.CrossRefGoogle Scholar
(15)Stallings, J. R.Quotients of the powers of the augmentation ideal in a group ring. Knots, Groups and 3-Manifolds, Annals of Math. Studies 84 (1975), 101–118.Google Scholar
(16)Zassenhaus, H.Ein Verfahren jeder endlichen p-Gruppe einen Lie-Ring mit der Charakteristik p zuzuordnen. Abh. Math. Semi. Univ. Hamburg 13 (1940), 200–207.CrossRefGoogle Scholar