Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-24T16:27:53.305Z Has data issue: false hasContentIssue false
  • English
  • Français

Approximate solutions of the general relativity field equations with a scalar meson field

Published online by Cambridge University Press:  24 October 2008

J. Hyde
J. Hyde
Affiliation:
Department of Mathematics, Imperial College, London, S.W. 7
Get access Rights & Permissions [Opens in a new window]

Extract

It was shown by Birkhoff ((1), p. 253) that every spherically symmetric solution of the field equations of general relativity for empty space,

may be reduced, by suitable coordinate transformations, to the static Schwarzschild form:

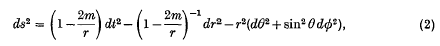
where m is a constant. This result is known as Birkhoff's theorem and excludes the possibility of spherically symmetric gravitational radiation. Different proofs of the theorem have been given by Eiesland(2), Tolman(3), and Bonnor ((4), p. 167).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 59 , Issue 4 , October 1963 , pp. 739 - 741
Copyright
Copyright © Cambridge Philosophical Society 1963

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Birkhoff, G. D.Relativity and modern physics (Harvard, 1927).CrossRefGoogle Scholar
(2)Eiesland, J.Trans. American Math. Soc. 27 (1925), 213.CrossRefGoogle Scholar
(3)Tolman, R. C.Relativity, thermodynamics and cosmology (Oxford, 1944).Google Scholar
(4)Bonnor, W. B. On Birkhoff's theorem: pp. 167–169 of Recent developments in general relativity (Pergamon; London, 1962).Google Scholar
(5)Hoffman, B.Quart. J. Math. Oxford Ser. 2, 3 (1932), 226.Google Scholar
(6)Hoffman, B.Quart. J. Math. Oxford Ser. 2, 4 (1933), 179.Google Scholar
(7)Hoffman, B. On the extension of Birkhoff's theorem to the case in which an electro-magnetic field is present: pp. 279–282 of Recent developments in general relativity (Pergamon; London, 1962).Google Scholar
(8)Das, A.Progr. Theoret. Phys. 24 (1960), 915.CrossRefGoogle Scholar
(9)Stephenson, G.Proc. Cambridge Philos. Soc. 58 (1962), 521.CrossRefGoogle Scholar