Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-24T17:00:25.526Z Has data issue: false hasContentIssue false
  • English
  • Français

Applications of the theory of cluster sets to a class of meromorphic functions

Published online by Cambridge University Press:  24 October 2008

E. F. Collingwood  and
A. J. Lohwater
E. F. Collingwood
Affiliation:
Lilburn Tower Alnwick Northumberland
A. J. Lohwater
Affiliation:
University of Michigan and University of Helsinki
Get access Rights & Permissions [Opens in a new window]

Extract

Let f (z) be meromorphic and non-rational in the domain |z| < R ≤ ∞, and let a be an arbitrary complex number, which may be infinite. The deficiency δ(a) of the value a is defined by

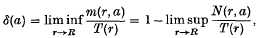
where m(r, a), N(r, a) and T(r) are defined as usual (cf. (10), pp. 156 ff.). For the class of functions considered in this paper the characteristic function T(r) is unbounded, and this will be assumed throughout. The upper (or Valiron) deficiency (16) of the value a is denned by

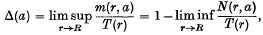
from which it follows that 0 ≤ δ(a) ≤ Δ(a) ≤ 1. A value a for which Δ(a) > 0 is called exceptional or deficient, and a value for which Δ(a) = 0 is called normal. We shall denote by G[a, σ] the open set of all values z in | z | < R for which | f(z) – a | < σ, where σ is a given positive number; we shall say that a component Gn[a, σ] of G[a, a] is bounded if the closure G¯n[a, σ] is contained in | z | < R, otherwise Gn[a, σ] will be called unbounded. In the case a = ∞, it is natural to define Gn[∞, σ] as the set of all z for which | f(z) | > 1/σ.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 53 , Issue 1 , January 1957 , pp. 93 - 105
Copyright
Copyright © Cambridge Philosophical Society 1957

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Beurling, A. Études sur un probleme de majoration, Thèse (Uppsala, 1931).Google Scholar
(2)Brelot, M.Sur l'allure à la frontière des fonctions harmoniques, sousharmoniques ou. holomorphes. Bull. Soc. Roy. Sci. Liège (1939), pp. 468–77.Google Scholar
(3)Carathéodory, C.Zum Schwarzschen Spiegelungsprinzip. Comment. Math. Helvet. 19 (1947), 263–78.Google Scholar
(4)Collingwood, E. F.Exceptional values of meromorphic functions. Trans. Amer. Math. Soc. 66 (1949), 308–46.Google Scholar
(4a)Collingwood, E. F.A theorem on prime ends. J. Land. Math. Soc. 31 (1956), 344–9.Google Scholar
(5)Collingwood, E. F. and Cartwright, M. L.Boundary theorems for a function meromorphic in the unit circle. Acta Math. 87 (1952), 83–146.Google Scholar
(5a)Collingwood, E. F. and Lohwater, A. T.Inégalités relatives aux défauts d'une fonction méromorphe dans le cercle-unité. C.R. Acad. Sci., Paris, 242 (1955), 1255–7.Google Scholar
(6)Gross, W.Zum Verhalten analytiseher Funktionen in der Umgebung singulärer Stellen. Math. Z. 2 (1918), 243–94.CrossRefGoogle Scholar
(7)Hössjer, G. and Frostman, O.Über die Ausnahmestellen eines Blaschkeproduktes. Medd. Lunds Univ. Mat. Semin. 1 (1933).Google Scholar
(8)Iversen, F.Zum Verhalten analytiseher Funktionen in Bereichen, deren Rand eine wesentliche Singularität enthält. Ofversigt Vet.-Soc. Förh. 44A (4) (1921).Google Scholar
(9)Kunugui, K.Sur un théorème de MM. Seidel-Beurling. Proc. Japan Acad. 15 (1939), 27–32.Google Scholar
(10)Nevanlinna, R.Eindeutige analytische Funktionen, 1st ed. (Berlin, 1936).CrossRefGoogle Scholar
(11)Noshiro, K.Note on the cluster sets of analytic functions. J. Math. Soc. Japan, 1 (1950), 275–81.Google Scholar
(12)Seidel, W.On the distribution of values of bounded analytic functions. Trans. Amer. Math. Soc. 36 (1934), 201–26.Google Scholar
(13)Selberg, H. L.Über einen Satz von Collingwood. Arch. Math. Naturvid. B, 47 (1944), No. 9.Google Scholar
(14)Selberg, H. L.Eine Ungleichung der Potentialtheorie und ihre Anwendung in der Theorie der meromorphen Funktionen. Comment. Math. Helvet. 18 (1946), 309–26.CrossRefGoogle Scholar
(15)Tsuji, M.On the cluster set of a meromorphic function. Proc. Japan Acad. 19 (1943), 60–5.Google Scholar
(16)Valibon, G.Sur la distribution des valeurs des fonctions méromorphes. Acta Math. 47 (1925), 117–142.CrossRefGoogle Scholar
(17)Valiron, G.Sur les singularités des fonctions holomorphes dans un cercle. C.R. Acad. Sci., Paris, 198 (1934), 2065–7.Google Scholar
(18)Valiron, G.Sur les singularités de certaines fonctions holomorphes et de leurs inverses. J. Math. pures appl. (3) 15 (1936), 423–35.Google Scholar