Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ball, John M.
1976.
Convexity conditions and existence theorems in nonlinear elasticity.
Archive for Rational Mechanics and Analysis,
Vol. 63,
Issue. 4,
p.
337.
1979.
Inequalities - Theory of Majorization and Its Applications.
Vol. 143,
Issue. ,
p.
531.
1987.
Measurement Error Models.
p.
409.
Lewis, A. S.
1996.
Convex Analysis on the Hermitian Matrices.
SIAM Journal on Optimization,
Vol. 6,
Issue. 1,
p.
164.
Lewis, Adrian S.
and
Overton, Michael L.
1996.
Eigenvalue optimization.
Acta Numerica,
Vol. 5,
Issue. ,
p.
149.
Lewis, A. S.
1996.
Group Invariance and Convex Matrix Analysis.
SIAM Journal on Matrix Analysis and Applications,
Vol. 17,
Issue. 4,
p.
927.
Seeger, Alberto
1997.
Convex Analysis of Spectrally Defined Matrix Functions.
SIAM Journal on Optimization,
Vol. 7,
Issue. 3,
p.
679.
Tam, Tin-Yau
1998.
Partial Superdiagonal Elements and Singular Values of a Complex Skew-Symmetric Matrix.
SIAM Journal on Matrix Analysis and Applications,
Vol. 19,
Issue. 3,
p.
737.
1999.
Directional Statistics.
p.
395.
Oskoorouchi, Mohammad R.
and
Goffin, Jean-Louis
2003.
The Analytic Center Cutting Plane Method with Semidefinite Cuts.
SIAM Journal on Optimization,
Vol. 13,
Issue. 4,
p.
1029.
Correa, Rafael
and
C., Hector Ramirez
2004.
A Global Algorithm for Nonlinear Semidefinite Programming.
SIAM Journal on Optimization,
Vol. 15,
Issue. 1,
p.
303.
Bebiano, N.
Nakazato, H.
da Providência, J.
Lemos, R.
and
Soares, G.
2005.
Inequalities for J-Hermitian matrices.
Linear Algebra and its Applications,
Vol. 407,
Issue. ,
p.
125.
Oskoorouchi, Mohammad R.
and
Goffin, Jean-Louis
2005.
An Interior Point Cutting Plane Method for the Convex Feasibility Problem with Second-Order Cone Inequalities.
Mathematics of Operations Research,
Vol. 30,
Issue. 1,
p.
127.
Piotrowski, Tomasz
and
Yamada, Isao
2008.
MV-PURE Estimator: Minimum-Variance Pseudo-Unbiased Reduced-Rank Estimator for Linearly Constrained Ill-Conditioned Inverse Problems.
IEEE Transactions on Signal Processing,
Vol. 56,
Issue. 8,
p.
3408.
Bebiano, N.
Nakazato, H.
and
da Providência, J.
2009.
On the Courant–Fischer theory for Krein spaces.
Linear Algebra and its Applications,
Vol. 430,
Issue. 7,
p.
1867.
Hamsici, O.C.
and
Martinez, A.M.
2009.
Rotation Invariant Kernels and Their Application to Shape Analysis.
IEEE Transactions on Pattern Analysis and Machine Intelligence,
Vol. 31,
Issue. 11,
p.
1985.
Niezgoda, Marek
2009.
Translation-invariant maps and applications.
Journal of Mathematical Analysis and Applications,
Vol. 354,
Issue. 1,
p.
111.
Gowda, M. Seetharama
and
Tao, J.
2011.
The Cauchy interlacing theorem in simple Euclidean Jordan algebras and some consequences.
Linear and Multilinear Algebra,
Vol. 59,
Issue. 1,
p.
65.
Di You
Hamsici, O C
and
Martinez, A M
2011.
Kernel Optimization in Discriminant Analysis.
IEEE Transactions on Pattern Analysis and Machine Intelligence,
Vol. 33,
Issue. 3,
p.
631.
Carson, William R.
Chen, Minhua
Rodrigues, Miguel R. D.
Calderbank, Robert
and
Carin, Lawrence
2012.
Communications-Inspired Projection Design with Application to Compressive Sensing.
SIAM Journal on Imaging Sciences,
Vol. 5,
Issue. 4,
p.
1185.


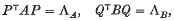
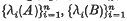 are each in descending order. (Thus we may say that the latent vectors of
are each in descending order. (Thus we may say that the latent vectors of 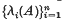 and
and  in order of occurrence be respectively
in order of occurrence be respectively 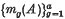 and
and 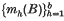 , so that
, so that