An arithmetic characterization of algebraic number fields with a given class group

Extract

Let R be the ring of integers of a number field K with class group G. It is classical that R is a unique factorization domain if and only if G is the trivial group; and the finite abelian group G is generally considered as a measure of the failure of unique factorization in R. The first arithmetic description of rings of integers with non-trivial class groups was given in 1960 by L. Carlitz (1). He proved that G is a group of order ≤ two if and only if any two factorizations of an element of R into irreducible elements have the same number of factors. In ((6), p. 469, problem 32) W. Narkiewicz asked for an arithmetic characterization of algebraic number fields K with class numbers ≠ 1, 2. This problem was solved for certain class groups with orders ≤ 9 in (2), and for the case that G is cyclic or a product 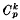of k copies of a group of prime order in (5). In this note we solve Narkiewicz's problem in general by giving arithmetical characterizations of a ring of integers whose class group G is any given finite abelian group.