No CrossRef data available.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Published online by Cambridge University Press: 24 October 2008
We may summarize our conclusions as follows. If the rotating doublets have quite different angular velocitiesinitially, then they repel each other with a force (R) given by
where
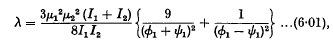
and
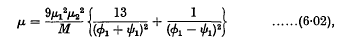
ø1 and ψ1 being the (constant) angular velocities of the two doublets.
If the doublets have the same angular velocities initially, and the same moments of inertia, then over a certain range of r we have
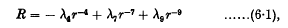
where
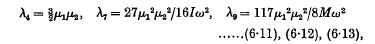
and ω is the common value of the angular velocities of the doublets. When the doublets correspond to hydrogen atoms in their principal quantum orbits, the range of distance becomes 5 Å. to 50 Å. and the formula for R reduces to
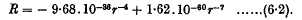
This is a law of force of the type found empirically by Lennard-Jones for helium, neon, and argon. The attractive term in this formula is larger than the attractive terms found by Lennard-Jones. The repulsive term, however, which leads to a “diameter” of 3·31 Å., is in very satisfactory agreement with the repulsive terms found by Lennard-Jones.
* Debye, P., “Molekularkräfte und ihre elektrische Deutung, § 6,” Phys. Zeit., vol. xxii, p. 306 (1921).Google Scholar
† P. Debye, loc. cit.
‡ Jones, J. E., Proc. Roy. Soc. A, vol. cvi, pp. 441, 463, 709 (1924); vol. cvii, p. 157 (1925)CrossRefGoogle Scholar; Lennard-Jones, J. E. and Taylor, P. A., Proc. Soy. Soc. A, vol. cix, p. 476 (1925).CrossRefGoogle Scholar
* This is possible as regards (φ1 + ψ1) t, but not as regards (φ1 + ψ1) t, when the doublets represent normal Bohr hydrogen atoms, rotating in the same sense, and whose relative velocity is the kinetic theory velocity appropriate to a temperature of 0°C. For then the distance travelled in 30 periods of revolution of the doublets is about 
of the radius of a hydrogen atom, and hence a considerably smaller fraction of the distance apart of the two doublets. To make a suitable choice of τ possible as regards both (φ1 + ψ1) t and (φ1 + ψ1) t we should have to make our doublets correspond to hydrogen atoms with different quantum numbers.
* For justification of these approximations see footnote on p. 281.Google Scholar
* We have already seen that this choice of τ is possible when the doublets represent normal hydrogen atoms.
* If the average value of
is not exactly zero, it will be very small compared with unity, and the coefficient of 
in equation(4.4) is only about 
or ¼ of the corresponding coefficient of r −n in the terms independent of 
* This condition is always fulfilled when the doublets represent hydrogen atoms, for two hydrogen atoms would only have the same initial angular velocities if they had the same quantum numbers, and then they would have the same moments of inertia.
† Numerical results are calculated from formulae and data given by Sommerfeld, Atomic Structure and Spectral Lines (transl. Brose), and Jeans, Dynamical Theory of Gases (3rd ed.).
‡ a = 0.532 A. Even if r were only 10a, τ1 would be 30τ′.
* The case of one doublet gaining complete revolutions on the other, corresponding to the equivalent pendulum swinging right round, would be represented in the analysis by γ imaginary or.
* I.e. the absolute value of ɛ, when ɛ is taken to satisfy.
* This statement justifies the expansions of
in § 4 in the case when the rotating doublets represent normal Bohr hydrogen atoms, for we only require these expansions to be true for moderately few periods of revolution of each atom including the time t=0; hence ξt is small compared with γ, itself less than π.
* Jones, J. E., Proc. Soy. Soc. A, voi. ovi, pp. 452et seq. (1924).Google Scholar