Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-27T19:06:38.322Z Has data issue: false hasContentIssue false
  • English
  • Français

Alternating projections between a strip and a halfplane

Published online by Cambridge University Press:  24 October 2008

Maciej Skwarczyński
Maciej Skwarczyński
Affiliation:
Smoleńskiego 27 A m.14, 01-698 Warszawa, Poland
Get access Rights & Permissions [Opens in a new window]

Extract

In a previous paper [6] the Bergman projection in D = A ∪ B, the union of domains A, B ⊂ CN, was described by alternating projections procedure. It was shown that when N = 1, and A, B are two halfplanes, the procedure can be carried out by explicit analytic calculations. In the present paper we show that the same is true for A = {|Re z| < π} and B = {Re z > 0}. In this case the calculations are more involved, and an essential use is made of L2-theorems of Paley–Wiener type due to T. Genchev, M. Dzrbasjan and W. Martirosjan. Of central importance is an operator W which maps f(z) onto 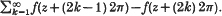. We show that for every g ∈ L2H(B) the sequence Wng (n = 1, 2, …) converges to zero locally uniformly in B.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 102 , Issue 1 , July 1987 , pp. 121 - 129
Copyright
Copyright © Cambridge Philosophical Society 1987

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Bergman, S.. The Kernel Function and Conformal Mapping, 2nd ed. Math. Surveys 5 (Amer. Math. Soc. 1970).Google Scholar
[2] Dzrbasjan, M.. Interpolation and spectral expansions associated with differential operators of fractional order [in Russian]. Izv. Akad. Nauk Armyan. SSR, Ser. Mat. 19 (1984), 81–181.Google Scholar
[3] Dzrbasjan, M., private communication, August 1984.Google Scholar
[4] Genchev, T.. Paley-Wiener type theorems for functions holomorphic in a half-plane. C. R. Acad. Bulgare Sci. 37 (1983), 141–144.Google Scholar
[5] Ryzik, I. and Gradstein, I.. Tables of Integrals, Sums, Series and Products [in Russian] (Moscow, 1951).Google Scholar
[6] Skwarczyński, M.. Alternating projections in complex analysis. Complex Analysis and Applications '83 (Sofia, 1985).Google Scholar
[7] Skwarczyński, M.. A general description of the Bergman projection. Ann. Polon. Math. 46 (volume in honour of F. Leja, 1985), 311–315.CrossRefGoogle Scholar