Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-25T01:02:15.584Z Has data issue: false hasContentIssue false
  • English
  • Français

Almost periodic generalized functions

Published online by Cambridge University Press:  24 October 2008

H. Burkill  and
B. C. Rennie
H. Burkill
Affiliation:
University of Sheffield
B. C. Rennie
Affiliation:
James Cook University of North Queensland
Get access Rights & Permissions [Opens in a new window]

Extract

In (4) a space C of generalized functions was defined which is rather larger than the simple space used to such effect by Lighthill in (3). At the core of C is the space C0 = T of test functions. These are entire (complex) functions f such that all derivatives of f and its Fourier transform F have order of magnitude not exceeding 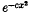as x → ± ∞, where c is a positive number depending on the individual derivative concerned. If f, g∈ T, the inner product 〈f | g〉 is defined to be

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 94 , Issue 1 , July 1983 , pp. 149 - 166
Copyright
Copyright © Cambridge Philosophical Society 1983

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Besicovitch, A. S.Almost periodic functions (Cambridge University Press, 1932).Google Scholar
(2)Doherty, I. W. Almost periodic generalized functions (Ph.D. thesis, University of Melbourne, 1973).Google Scholar
(3)Lighthill, M. J.Fourier analysis and generalised functions (Cambridge University Press, 1958).Google Scholar
(4)Rennie, B. C.On generalized functions. J. App. Prob. 19 A (1982), 139–156.CrossRefGoogle Scholar
(5)Schwartz, L.Théorie des distributions, vol. 2 (Hermann, Paris, 1951).Google Scholar