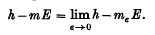Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Volkmann, Bodo
1956.
�ber Hausdorffsche Dimensionen von Mengen, die durch Zifferneigenschaften charakterisiert sind. V..
Mathematische Zeitschrift,
Vol. 65,
Issue. 1,
p.
389.
Beardon, A. F.
1965.
On the Hausdorff dimension of general Cantor sets.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 61,
Issue. 3,
p.
679.
Hatano, Kaoru
1968.
Evaluation of Hausdorff measures of generalized Cantor sets.
Hiroshima Mathematical Journal,
Vol. 32,
Issue. 2,
Hatano, Kaoru
1971.
Notes on Hausdorff dimensions of Cartesian product sets.
Hiroshima Mathematical Journal,
Vol. 1,
Issue. 1,
Borosh, I.
and
Fraenkel, A. S.
1975.
A generalization of Jarník’s theorem on Diophantine approximations to Ridout type numbers.
Transactions of the American Mathematical Society,
Vol. 211,
Issue. 0,
p.
23.
Zakharov, I. P.
and
Portnov, L. E.
1981.
Hausdorff dimensions of cartesian products.
Siberian Mathematical Journal,
Vol. 22,
Issue. 1,
p.
68.
Coppel, W. A.
1983.
An Interesting Cantor Set.
The American Mathematical Monthly,
Vol. 90,
Issue. 7,
p.
456.
Hata, Masayoshi
1985.
On the structure of self-similar sets.
Japan Journal of Applied Mathematics,
Vol. 2,
Issue. 2,
p.
381.
Cvitanović, Predrag
Jensen, Mogens H.
Kadanoff, Leo P.
and
Procaccia, Itamar
1985.
Renormalization, unstable manifolds, and the fractal structure of mode locking.
Physical Review Letters,
Vol. 55,
Issue. 4,
p.
343.
Falconer, K. J.
1986.
Random fractals.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 100,
Issue. 3,
p.
559.
Hardin, D. P.
and
Massopust, P. R.
1986.
The capacity for a class of fractal functions.
Communications in Mathematical Physics,
Vol. 105,
Issue. 3,
p.
455.
Masel/ko, J.
and
Swinney, Harry L.
1986.
Complex periodic oscillations and Farey arithmetic in the Belousov–Zhabotinskii reaction.
The Journal of Chemical Physics,
Vol. 85,
Issue. 11,
p.
6430.
Mauldin, R. D.
1986.
Dimensions and Entropies in Chaotic Systems.
Vol. 32,
Issue. ,
p.
28.
Richetti, P.
Roux, J. C.
Argoul, F.
and
Arneodo, A.
1987.
From quasiperiodicity to chaos in the Belousov–Zhabotinskii reaction. II. Modeling and theory.
The Journal of Chemical Physics,
Vol. 86,
Issue. 6,
p.
3339.
BARNSLEY, MICHAEL F.
MASSOPUST, PETER
STRICKLAND, HENRY
and
SLOAN, ALAN D.
1987.
Fractal Modeling of Biological Structures.
Annals of the New York Academy of Sciences,
Vol. 504,
Issue. 1,
p.
179.
Falconer, K. J.
1987.
The Hausdorff dimension of some fractals and attractors of overlapping construction.
Journal of Statistical Physics,
Vol. 47,
Issue. 1-2,
p.
123.
Scheffer, Vladimir
1987.
Nearly one dimensional singularities of solutions to the Navier-Stokes inequality.
Communications in Mathematical Physics,
Vol. 110,
Issue. 4,
p.
525.
Graf, Siegfried
1987.
Statistically self-similar fractals.
Probability Theory and Related Fields,
Vol. 74,
Issue. 3,
p.
357.
Falconer, K. J.
1988.
The Hausdorff dimension of self-affine fractals.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 103,
Issue. 2,
p.
339.
Mauldin, R. Daniel
and
Williams, S. C.
1988.
Hausdorff dimension in graph directed constructions.
Transactions of the American Mathematical Society,
Vol. 309,
Issue. 2,
p.
811.
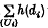 for any such sequence {Ui}. Then h–mεE is non-decreasing as ε tends to zero. We define
for any such sequence {Ui}. Then h–mεE is non-decreasing as ε tends to zero. We define