Hostname: page-component-745bb68f8f-kw2vx Total loading time: 0 Render date: 2025-01-08T11:35:38.174Z Has data issue: false hasContentIssue false
  • English
  • Français

Additive correlation and the inverse problem for the large sieve

Published online by Cambridge University Press:  09 July 2018

BRANDON HANSON
BRANDON HANSON*
Affiliation:
Dept. of Mathematics, Boyd Graduate Studies Research Center, University of Georgia, Athens, GA 30602, USA. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let A ⊆ [1, N] be a set of integers with |A| ≫ 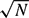$\sqrt N$. We show that if A avoids about p/2 residue classes modulo p for each prime p, then A must correlate additively with the squares S = {n2 : 1 ≤ n ≤ 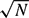$\sqrt N$}, in the sense that we have the additive energy estimate

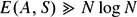$$ E(A,S)\gg N\log N. $$
This is, in a sense, optimal.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 168 , Issue 2 , March 2020 , pp. 211 - 217
Copyright
Copyright © Cambridge Philosophical Society 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[BC] Bose, R. C. and Chowla, S. Theorems in the additive theory of numbers. Comment. Math. Helv. 37 (1962-63), 141–147.Google Scholar
[CL] Croot, E. S. III, and Lev, V. F. Open problems in additive combinatorics. In Additive combinatorics, volume 43 of CRM Proc. Lecture Notes, pages 207–233 (Amer. Math. Soc., Providence, RI, 2007).Google Scholar
[FI] Friedlander, J. and Iwaniec, H. Opera de cribro. American Mathematical Society Colloquium Publications, 57 (American Mathematical Society, Providence, RI, 2010).Google Scholar
[GH] Green, B. and Harper, A. J Inverse questions for the large sieve. Geom. Funct. Anal. 24 (4) (2014), 1167–1203.Google Scholar
[HV] Helfgott, H. A. and Venkatesh, A. How small must ill-distributed sets be? Analytic Number Theory, Essays in honour of Klaus Roth (Cambridge University Press 2009), 224–234.Google Scholar
[K] Kolountzakis, M. N. On the uniform distribution in residue classes of dense sets of integers with distinct sums. J. Number Theory 76 (1999), 147–153.Google Scholar
[La] Landau, E. Über die Einteilung der positiven ganzen Zahlen in vier Klassen nach der Mindeszahl der zu ihrer additiven Zusammensetzung erforderlichen Quadrate. Arch. Math. Phys. 13 (1908), 305–312.Google Scholar
[Li] Lindström, B. Well distribution of Sidon sets in residue classes. J. Number Theory 69 (1998), 197–200.Google Scholar
[M] Montgomery, H. L. A note on the large sieve. J. London Math. Soc. 43 (1968), 93–98.Google Scholar
[R] Ramanujan, S. Some formulae in the analytic theory of numbers. Messenger Math. 45 (1916), 81–84.Google Scholar
[W1] Walsh, M. N. The inverse sieve problem in high dimensions. Duke Math. J. 161 (2012), no. 10, 2001–2022.Google Scholar
[W2] Walsh, M. N. The algebraicity of ill-distributed sets. Geom. Funct. Anal. 24 (2014), no. 3, 959–967.Google Scholar