Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-27T02:54:24.479Z Has data issue: false hasContentIssue false
  • English
  • Français

Zeros of the Epstein zeta function to the right of the critical line

Part of: Zeta and $L$-functions: analytic theory Forms and linear algebraic groups

Published online by Cambridge University Press:  17 November 2020

YOUNESS LAMZOURI
YOUNESS LAMZOURI*
Affiliation:
Institut Élie Cartan de Lorraine, Université de Lorraine, BP 70239, 54506 Vandoeuvre-lès-Nancy Cedex, France; and Department of Mathematics and Statistics, York University, 4700 Keele Street, Toronto, ON, M3J1P3Canada. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let E(s, Q) be the Epstein zeta function attached to a positive definite quadratic form of discriminant D < 0, such that h(D) ≥ 2, where h(D) is the class number of the imaginary quadratic field 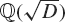${\mathbb{Q}} (\sqrt D)$. We denote by 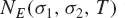${N_E}({\sigma _1},{\sigma _2},T)$ the number of zeros of 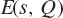$[E(s,Q)$ in the rectangle 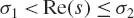${\sigma _1} < {\mathop{\rm Re}\nolimits} (s) \le {\sigma _2}$ and 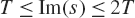$T \le {\mathop{\rm Im}\nolimits} (s) \le 2T$, where 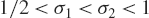$1/2 < {\sigma _1} < {\sigma _2} < 1$ are fixed real numbers. In this paper, we improve the asymptotic formula of Gonek and Lee for 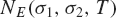${N_E}({\sigma _1},{\sigma _2},T)$, obtaining a saving of a power of log T in the error term.

MSC classification

Primary: 11E45: Analytic theory (Epstein zeta functions; relations with automorphic forms and functions) 11M41: Other Dirichlet series and zeta functions
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 171 , Issue 2 , September 2021 , pp. 265 - 276
Copyright
© Cambridge Philosophical Society 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

Partially supported by a Discovery Grant from the Natural Sciences and Engineering Research Council of Canada.

References

REFERENCES

Bombieri, E. and Hejhal, D.. On the distribution of zeros of linear combinations of Euler products. Duke Math. J. 80 (1995), 821–862.CrossRefGoogle Scholar
Borchsenius, V. and Jessen, B.. Mean motions and values of the Riemann zeta function. Acta Math. 80 (1948), 97–166.CrossRefGoogle Scholar
Davenport, H. and Heilbronn, H.. On the zeros of certain Dirichlet series. J. London Math. Soc. 11 (1936), 181–185, 307–312.CrossRefGoogle Scholar
Epstein, P.. Zur Theorie allgemeiner Zetafunctionen. Math. Ann. 56, 615–644 (1903).CrossRefGoogle Scholar
Gonek, S. and Lee, Y.. Zero-density estimates for Epstein zeta functions. Q. J. Math. 68 (2017), no. 2, 301–344.Google Scholar
Lamzouri, Y., Lester, S., and Radziwill, M.. Discrepancy bounds for the distribution of the Riemann zeta-function and applications. J. Anal. Math. 139 (2019), no. 2, 453–494.Google Scholar
Lee, Y.. On the zeros of Epstein zeta functions. Forum Math 26 (2014), 1807–1836.CrossRefGoogle Scholar
Lee, Y.. Zero-density estimates for Epstein zeta functions of class numbers 2 or 3. J. Korean Math. Soc. 54 (2017), no. 2, 479–491.Google Scholar
Titchmarsh, E. C.. The Theory of the Riemann Zeta-Function, 2nd ed. (Oxford University Press, Oxford, 1986) (Revised by D.R. Heath-brown).Google Scholar
Voronin, S. M.. The zeros of zeta-functions of quadratic forms (in Russian). Tr. Mat. Inst. Steklova 142 (1976), 135–147.Google Scholar