Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-27T02:35:03.606Z Has data issue: false hasContentIssue false
  • English
  • Français

Whitney equisingularity of families of surfaces in ℂ3

Published online by Cambridge University Press:  15 January 2018

M.A.S. RUAS  and
O.N. SILVA
M.A.S. RUAS
Affiliation:
Universidade de São Paulo - ICMC, Caixa Postal 668, 13560-970 São Carlos (SP), Brazil. e-mail: [email protected]
O.N. SILVA
Affiliation:
Universidad Nacional Autónoma de México, Instituto de Matemáticas, 62210, Cuernavaca (Mor), México. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we study families of singular surfaces in ℂ3 parametrised by 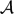$\mathcal {A}$-finitely determined map germs. We consider the topological triviality and Whitney equisingularity of an unfolding F of a finitely determined map germ f : (ℂ2, 0) → (ℂ3, 0). We investigate the following question: topological triviality implies Whitney equisingularity of the unfolding F? We provide a complete answer to this question, by giving counterexamples showing how the conjecture can be false.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 166 , Issue 2 , March 2019 , pp. 353 - 369
Copyright
Copyright © Cambridge Philosophical Society 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Callejas Bedregal, R., Houston, K. and Ruas, M.A.S. Topological triviality of families of singular surfaces. Preprint, arXiv:math/0611699v1 [math.CV] (2006).Google Scholar
[2] de Bobadilla, J. Fernández and Pe Pereira, M. Equisingularity at the normalisation. J. Topol. 88 (2008), 879–909.Google Scholar
[3] Damon, J. Topological triviality and versality for subgroups of A and K II. Sufficient conditions and applications. Nonlinearity 5 (1992), 373–412.Google Scholar
[4] Gaffney, T. Polar multiplicities and equisingularity of map germs. Topology 32 (1993), 185–223.Google Scholar
[5] Gibson, C. G., Wirthmüller, K., du Plessis, A. A. and Looijenga, E. J. N. Topological stability of smooth mappings. Springer LNM. 552 (1976), 71–88.Google Scholar
[6] Hernandes, M. E., Miranda, A. J. and Peñafort-Sanchis, G. A presentation matrix algorithm for f∗$\mathcal {O}$X,x. Preprint (2015).Google Scholar
[7] Marar, W.L. and Mond, D. Multiple point schemes for corank 1 maps. J. London Math. Soc. 39 (1989), 553–567.Google Scholar
[8] Marar, W. L. and Nuño–Ballesteros, J. J. Slicing corank 1 map germs from ℂ2 to ℂ3. Quart. J. Math. 65 (2014), 1375–1395.Google Scholar
[9] Marar, W. L., Nuño-Ballesteros, J. J. and Peñafort–Sanchis, G. Double point curves for corank 2 map germs from ℂ2 to ℂ3. Topology Appl. 159 (2012), 526–536.Google Scholar
[10] Miranda, A. J. https://sites.google.com/site/aldicio/publicacoes.Google Scholar
[11] Mond, D. On the classification of germs of maps from ℝ2 to ℝ3. Proc. London Math. Soc. 50 (1985), 333–369.Google Scholar
[12] Mond, D. Some remarks on the geometry and classification of germs of map from surfaces to 3-space. Topology 26 (1987), 361–383.Google Scholar
[13] Mond, D. and Pellikaan, R. Fitting ideals and multiple points of analytic mappings. In: Algebraic Geometry and Complex Analysis. Lecture Notes in Math. vol. 1414 (Springer, 1987), pp. 107–161.Google Scholar
[14] Mond, D. The number of vanishing cycles for a quasihomogeneous mapping from ℂ2 to ℂ3. Quart. J. Math. Oxford (2) 42 (1991), 335–345.Google Scholar
[15] Peñafort–Sanchis, G. Reflection Maps. Preprint, arXiv:1609.03222v2 [math.AG], (2016).Google Scholar
[16] Ruas, M.A.S. Equimultiplicity of topologically equisingular families of parametrised surfaces in ℂ3. Preprint, arXiv:1302.5800v1 [math.CV], (2013).Google Scholar
[17] Ruas, M.A.S. On the equisingularity of families of corank 1 generic germs. Contemporary Math. 161 (1994), 113–121.Google Scholar
[18] Silva, O.N. Superfícies com singularidades não isoladas. PhD thesis. Universidade de São Paulo (2017).Google Scholar
[19] Teissier, B. Sur la classification des singularités des espaces analytiques complexes. In Proceedings of the International Congress of Mathematicians vol. 1, 2 (Warsaw, 1983), pp. 763–781.Google Scholar
[20] Teissier, B. Variétés polaires II: multiplicités polaires, sections planes, et conditions de Whitney. In Algebraic Geometry, Proc. La Rabida. Lecture Notes in Math. vol. 961 (Springer–Verlag, 1982), pp. 314–491.Google Scholar
[21] Wall, C. T. C. Finite determinacy of smooth map-germs. Bull. London Math. Soc. (6) 13 (1981), 481–539.Google Scholar
[22] Wolfram, D., Greuel, G. M., Pfister, G. and Schönemann, H. Singular 4-0-2, a computer algebra system for polynomial computations. http://www.singular.uni-kl.de, (2015).Google Scholar