Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Damon, James
and
Mond, David
1991.
$$A$$ and the vanishing topology of discriminants.
Inventiones Mathematicae,
Vol. 106,
Issue. 1,
p.
217.
Mond, David
1995.
Looking at bent wires – -codimension and the vanishing topology of parametrized curve singularities.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 117,
Issue. 2,
p.
213.
Wall, C. T. C.
1996.
Algebraic Geometry and Singularities.
p.
277.
Bruce, J W
Kirk, N P
and
Plessis, A A du
1997.
Complete transversals and the classification of singularities.
Nonlinearity,
Vol. 10,
Issue. 1,
p.
253.
Saia, Marcelo Jose
1998.
Pre-weighted homogeneous map germs—Finite determinacy and topological triviality.
Nagoya Mathematical Journal,
Vol. 151,
Issue. ,
p.
209.
MOYA-PÉREZ, J.A.
and
NUÑO-BALLESTEROS, J.J.
2010.
The link of a finitely determined map germ from R2 to R2.
Journal of the Mathematical Society of Japan,
Vol. 62,
Issue. 4,
Hernandes, M.E.
Miranda, A.J.
and
Peñafort-Sanchis, G.
2018.
An algorithm to compute a presentation of pushforward modules.
Topology and its Applications,
Vol. 234,
Issue. ,
p.
440.
Nuño-Ballesteros, J. J.
Oréfice-Okamoto, B.
and
Tomazella, J. N.
2018.
Equisingularity of map germs from a surface to the plane.
Collectanea Mathematica,
Vol. 69,
Issue. 1,
p.
65.
Farnik, M.
Jelonek, Z.
and
Ruas, M. A. S.
2020.
Whitney theorem for complex polynomial mappings.
Mathematische Zeitschrift,
Vol. 295,
Issue. 3-4,
p.
1039.
FARNIK, Michał
JELONEK, Zbigniew
and
RUAS, Maria Aparecida Soares
2021.
Finite $\mathcal{A}$-determinacy of generic homogeneous map germs in $\mathbb{C}^3$.
Journal of the Mathematical Society of Japan,
Vol. 73,
Issue. 1,


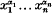 appearing in the Taylor expansion of the
appearing in the Taylor expansion of the