Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-25T01:28:39.771Z Has data issue: false hasContentIssue false
  • English
  • Français

The wave front set of the solution of a simple initial-boundary value problem with glancing rays

Published online by Cambridge University Press:  24 October 2008

F. G. Friedlander
F. G. Friedlander
Affiliation:
Department of Applied Mathematics and Theoretical Physics, Cambridge
Get access Rights & Permissions [Opens in a new window]

Extract

1. The singularities of solutions of linear partial differential equations are most appropriately described in terms of wave front sets of distributions. (For the definition and properties of wave front sets, see (4) and (5).) In particular, let Ω ⊂ RN be an open set and let P be a linear partial differential operator defined on Ω, with smooth coefficients, real principal symbol p(x, ξ), and simple characteristics. 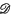Then if u ∈ ′ (Ω) and Pu = 0, the wave front set of u, WF(u), is a set in the cotangent bundle T*Ω (minus the zero section) that is contained in p−1(0) and is invariant under the flow generated in p−1(0) by the Hamiltonian vector field (gradξp, − gradxp). In other words, WF(u) is made up of bicharacteristic strips. This is a special case of an important theorem due to Hörmander (5), and Duistermaat and Hörmander (1), which generalizes classical results on the relation between discontinuities of solutions of a partial differential equation and the characteristics of the equation.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 79 , Issue 1 , January 1976 , pp. 145 - 159
Copyright
Copyright © Cambridge Philosophical Society 1976

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Duistermaat, J. J. and Hörmander, L.Fourier Integral Operators II. Acta Math. 128 (1972), 183–259.Google Scholar
(2)Erdélyi, A.Asymptotic expansions (Dover; New York, 1956).Google Scholar
(3)Friedlander, F. G.Sound pulses (Cambridge University Press, 1958).Google Scholar
(4)Hörmander, L.Fourier Integral Operators I. Acta Math. 127 (1971), 79–183.CrossRefGoogle Scholar
(5)Hörmander, L.On the existence and regularity of solutions of linear pseudo-differential equations. L'Enseignement Math. 17 (1971), 99–163.Google Scholar
(6)Nirenberg, L.Lectures on linear partial differential equations. Regional Conference Series 17, A.M.S., 1973.CrossRefGoogle Scholar
(7)Zauderer, E.Domains of dependence for mixed problems for wave equations. Arch. Rat. Mech. and Anal. 15 (1964), 69–78.Google Scholar