Published online by Cambridge University Press: 24 October 2008
This paper is closely related to Bar-Natan's work, and fills in some of the gaps in [1]. Following his analogy of the extension of knot invariants to knots with double points to the notion of multivariate calculus on polynomials, we introduce a new notation which facilitates the formulation of a Leibniz type formula for the product of two Vassiliev invariants. This leads us to see how Bar-Natan's co-product of chord diagrams corresponds to multiplication of Vassiliev invariants. We also include a proof that the multiplication in 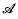 is a consequence of Bar-Natan's 4T relation.
is a consequence of Bar-Natan's 4T relation.
The last part of this paper consists of a proof that the space of weight systems is a sub-Hopf algebra of the space 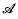 *, by means of the canonical projection.
*, by means of the canonical projection.