Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-25T02:13:51.173Z Has data issue: false hasContentIssue false
  • English
  • Français

The Vapour-Pressure Equations of Solutions and the Osmotic Pressure of Rubber

Published online by Cambridge University Press:  24 October 2008

A. R. Miller
A. R. Miller
Affiliation:
Gonville and Caius CollegeCambridge
Get access Rights & Permissions [Opens in a new window]

Extract

Assuming that the solute and solvent molecules in a solution can be regarded as occupying sites on a regular lattice and that the potential energy arises from interactions between molecules which occupy closest neighbour sites, the vapour-pressure equations have been determined for solutions in which each solute molecule contains three groups (or submolecules) and occupies three lattice sites in such a way that successive submolecules occupy closest neighbour sites on the lattice while each solvent molecule occupies only one site. The vapour-pressure equations are compared with those which have already been obtained by Fowler and Guggenheim for the case in which each solute molecule contains two submolecules in order to determine the effect on the form of the vapour-pressure equations of the number of submolecules in each solute molecule. This enables the determination of the vapour-pressure equations when each solute molecule contains n submolecules and occupies n lattice sites in such a way that successive submolecules occupy closest neighbour sites on the lattice. In this latter case the vapour-pressure equations are

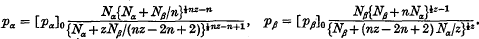
These equations are used to determine the osmotic pressure of solutions of long-chain polymers, and it is found that in the region of osmotic interest, the osmotic pressure is given by an equation of the form

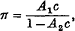
where c g. of solute per 100 c.c. of solution is the concentration. It is shown that this equation can be written approximately

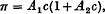
which is the quadratic relation which has usually been fitted to osmotic measurements. To this approximation π/c plotted as a function of c gives a straight line of which the intercept on the π/c axis determines the molecular weight of the polymer molecule and the gradient determines the number of submolecules in each polymer molecule.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 39 , Issue 1 , March 1943 , pp. 54 - 67
Copyright
Copyright © Cambridge Philosophical Society 1943

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Guggenheim, E. A.Proc. Roy. Soc. A, 135 (1932), 181.Google Scholar
(2)Guggenheim, E. A.Proc. Roy. Soc. A, 148 (1935), 304.Google Scholar
(3)Hildebrand, J. H.J. American Chem. Soc. 51 (1929), 69.Google Scholar
(4)Fowler, R. H.Statistical mechanics, 2nd ed. (Cambridge, 1936), p. 533 footnote.Google Scholar
(5)Rushbrooke, G. S.Proc. Roy. Soc. A, 166 (1938), 296.Google Scholar
(6)Fowler, R. H. and Rushbrooke, G. S.Trans. Faraday Soc. 33 (1937), 1272.CrossRefGoogle Scholar
(7)Chang, T. S.Proc. Cambridge Phil. Soc. 35 (1939), 293.Google Scholar
(8)Chang, T. S.Proc. Roy. Soc. A, 169 (1939), 512.Google Scholar
(9)Miller, A. R.Proc. Cambridge Phil. Soc. 38 (1942), 109.CrossRefGoogle Scholar
(10)Fowler, R. H. and Guggenheim, E. A.Statistical thermodynamics (Cambridge, 1939), § 821.Google Scholar
(11)Fowler, R. H.Statistical mechanics, 2nd ed. (Cambridge, 1936), § 5·41.Google Scholar
(12)See, for example, Guggenheim, E. A., Modern thermodynamics (Methuen, 1935), p. 85, equation (425).Google Scholar
(13)Posnjak, E.Kolloidchem. Beih. 3 (1912), 417.CrossRefGoogle Scholar
(14)Gee, G. and Treloar, L. R. G.Trans. Faraday Soc. 38 (1942), 147.CrossRefGoogle Scholar
(15)See, for example, Falkenhagen, H., Electrolytes, translated by Bell, R. P. (Oxford, 1934), § 6.Google Scholar