Published online by Cambridge University Press: 09 September 2016
Let π be a finite p-group and 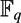 ${\mathbb{F}_{q}}$ a finite field with q = pn elements. Denote by
${\mathbb{F}_{q}}$ a finite field with q = pn elements. Denote by 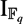 $\I_{\mathbb{F}_{q}}$ the augmentation ideal of the group ring
$\I_{\mathbb{F}_{q}}$ the augmentation ideal of the group ring 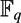 ${\mathbb{F}_{q}}$[π]. We have found a surprising relation between the abelianization of 1 +
${\mathbb{F}_{q}}$[π]. We have found a surprising relation between the abelianization of 1 + 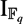 $\I_{\mathbb{F}_{q}}$, the Bogomolov multiplier B0(π) of π and the number of conjugacy classes k(π) of π:
In particular, if π is a finite p-group with a non-trivial Bogomolov multiplier, then 1 +
$\I_{\mathbb{F}_{q}}$, the Bogomolov multiplier B0(π) of π and the number of conjugacy classes k(π) of π:
In particular, if π is a finite p-group with a non-trivial Bogomolov multiplier, then 1 + 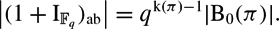 $$
\left | (1+\I_{\Fq})_{\ab} \right |=q^{\kk(\pi)-1}|\!\B_0(\pi)|.
$$
\left | (1+\I_{\Fq})_{\ab} \right |=q^{\kk(\pi)-1}|\!\B_0(\pi)|.
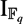 $\I_{\mathbb{F}_{q}}$ is a counterexample to the fake degree conjecture proposed by M. Isaacs.
$\I_{\mathbb{F}_{q}}$ is a counterexample to the fake degree conjecture proposed by M. Isaacs.