Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-25T13:05:06.715Z Has data issue: false hasContentIssue false
  • English
  • Français

Uniqueness theorems for analytic functions of one and of several complex variables

Published online by Cambridge University Press:  24 October 2008

L. A. Rubel  and
B. A. Taylor
L. A. Rubel
Affiliation:
University of Illinois
B. A. Taylor
Affiliation:
University of Illinois
Get access Rights & Permissions [Opens in a new window]

Extract

1. Suppose that f is a function analytic on a region G in complex n-space Cn, and that f(m)(w(m)) = 0 for each m = (m1, m2,…, mn), mi = 0, 1, 2,…, where

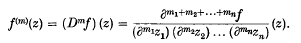
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 64 , Issue 1 , January 1968 , pp. 71 - 82
Copyright
Copyright © Cambridge Philosophical Society 1968

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Ålander, M. Sur le deplacement des zéros des fonctions entières par leur derivation, dissertation, Uppsala, 1914.Google Scholar
(2)Arsove, M. G.Paley-Wiener theorem in linear metric spaces. Pacific J. Math. 10 (1960), 365–379.CrossRefGoogle Scholar
(3)Boas, R. P.Expansions of analytic functions. Trans. Amer. Math. Soc. 48 (1940), 467–487.CrossRefGoogle Scholar
(4)Ebdös, P. and Rényi, A.On the number of zeros of successive derivatives of analytic functions. Acta Math. Acad. Sci. Hungar. 7 (1956), 125–144.Google Scholar
(5)Iyer, V. GanapathyOn singular functions. J. Indian Math. Soc. 8 (1944), 94–108.Google Scholar
(6)Gontcharoff, W.Recherches sur les derivées successives des fonctions analytiques. Ann. Sci. École Norm. Sup. 47 (1930), 1–78.CrossRefGoogle Scholar
(7)Kakeya, S.An extension of power series. Proc. Tokyo Phys. Math. Soc. 14 (1932), 125–138.Google Scholar
(8)Pólya, G.The zeros of the derivatives of a function. Bull. Amer. Math. Soc. 49 (1943), 178–191.CrossRefGoogle Scholar
(9)Takenaka, S.On the expansion of analytic functions in series of analytic functions and its application to the study of the distribution of zero points of the derivatives of analytic functions. Proc. Tokyo Phys. Math. Soc. ser. 3, 13 (1931), 111–132.Google Scholar
(10)Takenaka, S.On the expansion of integral transcendental functions in generalized Taylor7apos;s series. Proc. Tokyo Phys. Math. Soc. ser. 3, 14 (1932), 529–542.Google Scholar
(11)Wilf, H. S.Whittaker's constant for lacunary entire functions. Proc. Amer. Math. Soc. 14 (1963), 238–242.Google Scholar
(12)Džrbašjan, M. M.On the integral representation and expansion in generalized Taylor series of entire functions of several complex variables. Amer. Math. Soc. Translations, 2nd series, 32 (1963), 289–309.CrossRefGoogle Scholar
(13)Nguyen Thanh, Van.Sur l'interpolation d'Abel-Gontcharoff des fonctions entierès de n variables complexes. C.R. Acad. Sci., Paris 263 (1966), 782–784.Google Scholar
(14)Perami, Helene. Sur le problem d'Abel–Gontcharoff pour les fonctions entieres de deux variables. C.R. Acad. Sci. Paris 263 (1966), 566–569.Google Scholar