Two notes on the Riemann Zeta-function*
Published online by Cambridge University Press: 24 October 2008
Extract
Let Λ (n) be the arithmetic function usually so denoted, which is zero unless n is a prime power pm (m ≥ 1), when it is log p. We write as usual
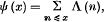
and
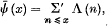
where the dash denotes that if x is an integer the last term Λ (x) of the sum is to be taken with a factor ½. We wrute further
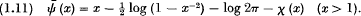
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 22 , Issue 3 , 20 September 1924 , pp. 234 - 242
- Copyright
- Copyright © Cambridge Philosophical Society 1924
References
† Landau, E., “Über einige Summen, die von den Nullstellen der Riemannschen Zetafunktion abhängen,” Acta Math., 35 (1911), pp. 271–294.CrossRefGoogle Scholar
‡ Our convention as to the use of O implies, of course, that the formula holds “uniformly for y ≥ √x.”
* I hope to publish this result shortly in another paper.
* Since all roots with γ > 0 lie in 0 < σ < 1, and are symmetrically disposed about the line σ = frac12;
† s 0 is a pure imaginary, and s describes the real axis as ζ describes the large rectangle.
* Here and in the argument below we use the inequality
A glance at the inequalities immediately following verifies the condition |z| < ½.
* Γ4 extends to the left (only) as far as σ = − 19.
† We naturally choose the determination of log ζ defined by the Dirichlet series for σ > 1.
- 10
- Cited by


