Two compounds of antiprisms in R⁴

Extract

A polygon is said to be uniform if and only if it is connected and regular. An n-dimensional polytope (n > 2) is called uniform if it has uniform cells and possesses a symmetry group transitive on the vertices. A polytope is either connected or a compound. If it is a compound we also require the components to be isomorphic and to have no cells of dimension ≥ n − 1 in common. The connected 3-dimensional uniform polytopes have been investigated by Coxeter, Longuet-Higgins and Miller (1). The convex 4-dimensional polytopes have been investigated by Conway and Guy (2). Compound polytopes have been less extensively described than connected polytopes, but see, for example, (3), (4). Based on 2- and 3-dimensional experience, one might navely conjecture: ‘given a symmetry group 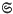, a uniform polytope P and an integer n, if a uniform compound polytope with symmetry group 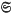and consisting of n copies of P exists, then it is either unique or else a member of a one-parameter family’.