Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-25T13:36:13.634Z Has data issue: false hasContentIssue false
  • English
  • Français

The transverse flexure of uniformly loaded curvilinear and rectilinear polygonal plates

Published online by Cambridge University Press:  24 October 2008

W. A. Bassali  and
F. R. Barsoum
W. A. Bassali
Affiliation:
University of Alexandria
F. R. Barsoum
Affiliation:
University of Alexandria
Get access Rights & Permissions [Opens in a new window]

Abstract

Complex variable methods are applied to derive exact solutions in closed forms for the small deflexions of uniformly loaded thin isotropic plates bounded by regular curvilinear polygonal contours having n sides. The supported boundary is either clamped or has equal boundary cross-couples. For rectilinear edges the latter conditions agree with those for a simply supported boundary. The plates taken in the z-plane are conformally mapped on the unit circle in the ζ-plane by the general mapping function

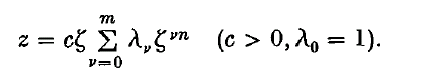
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 62 , Issue 3 , July 1966 , pp. 523 - 540
Copyright
Copyright © Cambridge Philosophical Society 1966

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Bassali, W. A.J. Mech. Phys. Solids 7 (1959), 145.CrossRefGoogle Scholar
(2)Bassali, W. A.Z. Angew. Math. Mech. 40 (1960), 493.CrossRefGoogle Scholar
(3)Bassali, W. A. and Hanna, N. O. M.Proc. Cambridge Philos. Soc. 57 (1961), 166.CrossRefGoogle Scholar
(4)Bassali, W. A. and Hanna, N. O. M.Bull. Calcutta Math. Soc. 53 (1961), 141.Google Scholar
(5)Bassali, W. A. and Dawoud, R. H.Proc. Cambridge Philos. Soc. 52 (1956), 584.CrossRefGoogle Scholar
(6)Conway, H. D.J. Appl. Mech. 27 (1960), 275.CrossRefGoogle Scholar
(7)Conway, H. D.J. Appl. Mech. 29 (1962), 755.CrossRefGoogle Scholar
(8)Deverall, L. I.J. Appl. Mech. 24 (1957), 295.CrossRefGoogle Scholar
(9)Greenberg, H. J. and Prager, W.Amer. J. Math. 120 (1948), 749.CrossRefGoogle Scholar
(10)Jahnke, E and Emde, F.Tables of functions with formulae and curves (Dover Publications; New York, 1945).Google Scholar
(11)Jones, P. D. Department of Supply, Australia, Report SM 252 (1957).Google Scholar
(12)Jones, P. D. Department of Supply, Australia, Report SM 260 (1958).Google Scholar
(13)Jones, P. D. Department of Supply, Australia, Report SM 266 (1959).Google Scholar
(14)Morley, L. S. D.Quart. J. Mech. Appl. Math. 15 (1962), 413.CrossRefGoogle Scholar
(15)Morley, L. S. D.Quart. J. Mech. Appl. Math. 16 (1963), 109.CrossRefGoogle Scholar
(16)Morley, L. S. D.Quart. J. Mech. Appl. Math. 17 (1964), 293.CrossRefGoogle Scholar
(17)Muskhelishvili, N. I.Some basic problems of the mathematical theory of elasticity, 3rd ed. (Moscow, 1949).Google Scholar
(18)Sen, B.Philos. Mag. 33 (1942), 294.CrossRefGoogle Scholar
(19)Seth, B. R.Proc. Indian Acad. Sci. Sect. 22 (1945), 234.CrossRefGoogle Scholar
(20)Seth, B. R.Philos. Mag. 38 (1947), 282.CrossRefGoogle Scholar
(21)Seth, B. R.Bull. Calcutta Math. Soc. 40 (1948), 36.Google Scholar
(22)Stevenson, A. C.Philos. Mag. 34 (1943), 105.CrossRefGoogle Scholar
(23)Timoshenko, S. and Woinowsky-Krieger, S.Theory of plates and shells, 2nd ed. (New York, 1959).Google Scholar
(24)Weinstein, A. and Rock, D. H.Quart. Appl. Math. 2 (1944), 262.CrossRefGoogle Scholar
(25)Winslow, A. M.Quart. J. Mech. Appl. Math. 10 (1957), 160.CrossRefGoogle Scholar
(26)Williams, M. L.U.S. Nat. Cong. Appl. Mech., Illinois Inst. of Technology (1951), 325.Google Scholar