Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-25T13:16:44.039Z Has data issue: false hasContentIssue false
  • English
  • Français

The trace form for tame, abelian extensions of number fields

Published online by Cambridge University Press:  24 October 2008

M. J. Taylor
M. J. Taylor
Affiliation:
Department of Mathematics, U.M.I.S.T., P.O. Box 88, Manchester, M60 1QD
Get access Rights & Permissions [Opens in a new window]

Extract

Let N/K be a tame, abelian extension of number fields, whose Galois group is denoted by Γ. The basic object of study in this paper is the ring of integers of N, endowed with the trace form TN/K; the pair is then a Hermitian module (where we abbreviate ), and it restricts to a -Hermitian module (The reader is referred to Section 2 for the basics on Hermitian modules.) Ideally one would like to determine completely the class of this Hermitian module in K0H(ℤΓ), the Grothendieck group of ℤΓ-Hermitian modules modulo orthogonal sums; however, in general when Γ is even, one knows that even the ℚΓ-Hermitian module given by restricting (N, TN/K) is difficult to classify. (See for instance [S] and [F2].) To circumvent this difficulty we proceed in the following fashion, as suggested by the recent work of P. Lawrence (see [L]): let D = D(Γ) denote the anti-diagonal of Γ in Γ × Γ, that is to say

and let N(2) = (N⊗KN)D so that N(2) is a Galois algebra over K with Galois group Γ × Γ/D(Γ) ≅ Γ. Write for the trace form of N(2)/K, and define the -order it is then easy to see that is isomorphic as an -module to (see (3·1·6)). To be precise we ought really to write 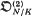etc.; however, the base field will always be clear from the context.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 119 , Issue 2 , February 1996 , pp. 209 - 230
Copyright
Copyright © Cambridge Philosophical Society 1996

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[B] Bayer, E., letter dated 22nd December, 1989.Google Scholar
[BL] Bayer, E. and Lenstra, H. W.. Forms in odd degree extensions and self-dual normal bases. Amer. J. Math. 112 (1990), 359–373.CrossRefGoogle Scholar
[BM] Bayer-Fluckiger, E. and Morales, J.. Sums of trace forms in number fields, preprint.Google Scholar
[BT] Byott, N. and Taylor, M. J.. Hopf orders and Galois module structure. In Group rings and classgroups (ed. Roggenkamp, K. and Taylor, M. J.), DMV Seminar 18 (Birkhaüser, 1992).Google Scholar
[E] Erez, B.. On the hermitian structure of Galois modules in number fields and Adams operations. Sem. Théorie des nombres, Paris, 1989–90, PM (Birkhaüser, 1992).CrossRefGoogle Scholar
[ET] Erez, B. and Taylor, M. J.. Hermitian modules in Galois extensions of number fields and Adams operations. Annals of Mathematics 135 (1992), 271–296.CrossRefGoogle Scholar
[F1] Fröhlich, A.. Classgroups and Hermitian modules. Pure Mathematics 48 (Birkhaüser, 1984).Google Scholar
[F2] Fröhlich, A.. Orthogonal representations of Galois groups, Stiefel-Whitney classes and Hasse-Witt invariants. J. reine angew. Math. 360 (1985), 84–123.Google Scholar
[F3] Fröhlich, A.. Galois module structure of algebraic integers. (Springer, 1983).CrossRefGoogle Scholar
[K] Kneser, M.. Strong approximation: In Proc. of Symposia in pure math., vol. IX (American Math. Soc. Providence, R.I., 1966).Google Scholar
[L] Lawrence, P.. The Hermitian structure of principal homogeneous spaces of groups schemes (Doctoral thesis, Manchester, 1992).Google Scholar
[M] Martinet, J.. Character theory and Artin L-functions. In Algebraic Number Fields, Proc. Durham Symposium (ed. Fröhlich, A.) (Academic Press, 1977).Google Scholar
[S] Serre, J.-P.. L'invariant de Witt de la forme Tr(x2). Comment. Helv. 59 (1984), 651–676.CrossRefGoogle Scholar
[T1] Taylor, M. J.. Rings of integers and trace forms for tame extensions of odd degree. Math. Zeit. 202 (1989), 313–341.CrossRefGoogle Scholar
[T2] Taylor, M. J.. On Fröhlich's conjecture for rings of integers of tame extensions. Inv. Math. 63 (1981), 41–79.CrossRefGoogle Scholar
[T3] Taylor, M. J.. Classgroups of group rings, LMS Lecture Notes 91 (Cambridge University Press, 1984).CrossRefGoogle Scholar