Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-25T13:44:26.944Z Has data issue: false hasContentIssue false
  • English
  • Français

A toral configuration space and regular semisimple conjugacy classes

Published online by Cambridge University Press:  24 October 2008

G. I. Lehrer
G. I. Lehrer
Affiliation:
School of Mathematics and Statistics, University of Sydney, Sydney, Australia2006
Get access Rights & Permissions [Opens in a new window]

Extract

For any topological space X and integer n ≥ 1, denote by Cn(X) the configuration space

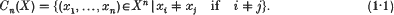
The symmetric group Sn acts by permuting coordinates on Cn(X) and we are concerned in this note with the induced graded representation of Sn on the cohomology space H*(Cn(X)) = ⊕iHi (Cn(X), ℂ), where Hi denotes (singular or de Rham) cohomology. When X = ℂ, Cn(X) is a K(π, 1) space, where π is the n-string pure braid group (cf. [3]). The corresponding representation of Sn in this case was determined in [5], using the fact that Cn(C) is a hyperplane complement and a presentation of its cohomology ring appears in [1] and in a more general setting, in [8] (see also [2]).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 118 , Issue 1 , July 1995 , pp. 105 - 113
Copyright
Copyright © Cambridge Philosophical Society 1995

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Arnold, V. I.. The cohomology ring of the coloured braid group. Math. Notes 5 (1969), 138–140.CrossRefGoogle Scholar
[2]Cohen, F.. The homology of Cn+1-spaces, n ≥ 0, in: The homology of iterated loop spaces, Springer L.N.M. 533 (eds. Cohen, F. R., Lada, T. J. and May, J. P.) (Springer Verlag, 1976), 207–352.CrossRefGoogle Scholar
[3]Deligne, P., Les immeubles des groupes de tresses géneralisés. Invent. Math. 17 (1972), 273–302.CrossRefGoogle Scholar
[4]Deligne, P. and Lusztig, G.. Representations of reductive groups over finite fields. Ann. of Math. 103, (1976), 103–161.CrossRefGoogle Scholar
[5]Lehrer, G. I.. On the Poincaré series associated with Coxeter group actions on complements of hyperplanes. J. London Math. Soc. (2) 36 (1987), 275–294.CrossRefGoogle Scholar
[6]Lehrer, G. I.. The l-adic cohomology of hyperplane complements. Bull. London Math. Soc. 24 (1992), 76–82.CrossRefGoogle Scholar
[7]Lehrer, G. I.. Rational tori, semisimple, orbits and the topology of hyperplane complements. Comment. Math. Helvetici 67 (1992), 226–251.CrossRefGoogle Scholar
[8]Orlik, P. and Solomon, L.. Combinatorics and the topology of complements of hyperplanes. Invent. Math. 56 (1980), 167–198.CrossRefGoogle Scholar