No CrossRef data available.
Published online by Cambridge University Press: 24 October 2008
This paper is a sequel to [6] and concerns the complex divisor function
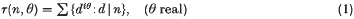
which has had a number of applications in the analytic theory of numbers. Thus Hooley's Δ-function [8] defined by
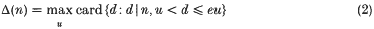
satisfies the inequality

and Erdös' τ+-function, defined by

satisfies