Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-25T14:02:21.480Z Has data issue: false hasContentIssue false
  • English
  • Français

Symmetries of generalized Klein-Gordon (including sine-Gordon) equations in three or more dimensions

Published online by Cambridge University Press:  24 October 2008

T. J. Gordon
T. J. Gordon
Affiliation:
Department of Engineering Mathematics, Loughborough University of Technology
Get access Rights & Permissions [Opens in a new window]

Extract

Much recent attention has been devoted to those nonlinear partial differential equations admitting higher-order conservation laws (e.g. [2] and references therein) or equivalently admitting higher-order symmetries. In particular the sine-Gordon equation 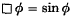possesses such symmetries [5, 7] where 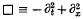is the two-dimensional d'Alembertian operator. The question posed and solved here is whether such behaviour is possible in higher dimensions. We therefore consider the ‘Generalized Klein–Gordon’ (GKG) equation

in N dimensions where 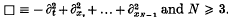and N ≥ 3.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 101 , Issue 2 , March 1987 , pp. 343 - 348
Copyright
Copyright © Cambridge Philosophical Society 1987

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Choquet-Bruhat, Y., de Witt-Morette, C. and Dillard-Bleick, M.. Analysis Manifolds and Physics (North-Holland, 1977).Google Scholar
[2]Drazin, P. G.. Solitons. London Mathematical Society lecture note series no. 85 (Cambridge University Press, 1983).CrossRefGoogle Scholar
[3]Gordon, T. J.. Conserved currents of the Klein–Gordon field. Math. Proc. Cambridge Philos. Soc. 90 (1981), 507–515.CrossRefGoogle Scholar
[4]Gordon, T. J.. Equivalent conserved currents and generalised Noether's theorem. Ann. Phys. (USA) 155 (1984), 85–107.CrossRefGoogle Scholar
[5]Sanuki, H. and Konno, K.. Conservation laws of sine-Gordon equation. Phys. Lett. 48 A (1974), 221–222.CrossRefGoogle Scholar
[6]Tsujishita, T.. Conservation laws of free Klein–Gordon fields. Lett. Math. Phys. 3 (1979), 445–450.CrossRefGoogle Scholar
[7]Tu, G. Z.. On polynomial symmetries of the sine-Gordon equation. Math. Proc. Cambridge Philos. Soc. 91 (1982), 485–489.CrossRefGoogle Scholar