No CrossRef data available.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Published online by Cambridge University Press: 24 October 2008
1. Let
be a numerical series. If for sufficiently small h > 0 the series
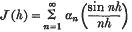
is convergent, we can form the upper and lower limits of J (h) as h → 0. These limits are called respectively the upper and lower sums (R, 1) of the series (1). For the purposes of the present paper it will be convenient to consider a more extended definition of these upper and lower sums. We shall suppose that for sufficiently small h the series J (h) is summable by Poisson's method. We denote the Poisson sum by PJ (h). The upper and lower limits of PJ (h) as h → 0 will be called the upper and lower sums (R, 1) of the series (1).
† Khintchine, , Fund. Math. 9 (1927), 212–279 (§ 1).CrossRefGoogle Scholar
* Proc. Lond. Math. Soc. 31 (1930), 373.Google Scholar
† Math. Zeit. 25 (1926), 274–290 (Theorem 1, Chap. II).Google Scholar