Sufficient Statistics and Orthogonal Parameters
Published online by Cambridge University Press: 24 October 2008
Extract
Let 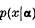 be, for a set of n real continuous parameters
be, for a set of n real continuous parameters 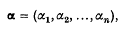 the probability density function of a random variable x with respect to a σ-finite measure μ on a σ-algebra of subsets of the sample space
the probability density function of a random variable x with respect to a σ-finite measure μ on a σ-algebra of subsets of the sample space 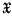 . If x; is a continuous random variable, μ will be Lebesgue measure on the Borel sets of a Euclidean sample space and, if x is discrete, μ will be counting measure on the class of all sets of a countable sample space. The parameters αi are said to be orthogonal (Jeffreys (3), pp. 158,184) if
. If x; is a continuous random variable, μ will be Lebesgue measure on the Borel sets of a Euclidean sample space and, if x is discrete, μ will be counting measure on the class of all sets of a countable sample space. The parameters αi are said to be orthogonal (Jeffreys (3), pp. 158,184) if 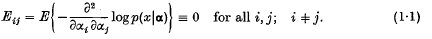 .
.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 58 , Issue 2 , April 1962 , pp. 326 - 337
- Copyright
- Copyright © Cambridge Philosophical Society 1962
References
REFERENCES
- 3
- Cited by


