Hostname: page-component-745bb68f8f-hvd4g Total loading time: 0 Render date: 2025-01-13T08:03:53.629Z Has data issue: false hasContentIssue false
  • English
  • Français

Stochastic independence in non-commutative probability theory

Published online by Cambridge University Press:  24 October 2008

Wulf Driessler  and
Ivan F. Wilde
Wulf Driessler
Affiliation:
Bedford College, London, NW 1 4NS
Ivan F. Wilde
Affiliation:
Bedford College, London, NW 1 4NS
Get access Rights & Permissions [Opens in a new window]

Abstract

For a family {Xα} of random variables over a probability space 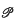, stochastic independence can be formulated in terms of factorization properties of characteristic functions. This idea is reformulated for a family {Aα} of selfadjoint operators over a probability gage space 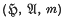and is shown to be inappropriate as a non-commutative generalization. Indeed, such factorization properties imply that the {Aα} mutually commute and are versions of independent random variables in the usual sense.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 86 , Issue 1 , July 1979 , pp. 103 - 114
Copyright
Copyright © Cambridge Philosophical Society 1979

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Batty, C. J. K.The strong law of large numbers for states and traces of a W*-algebra (Preprint, Math. Institute, Oxford).CrossRefGoogle Scholar
(2)Gootman, E. C. and Kannan, D.Zero-one laws in finite W*-algebras. J. Math. Anal. Appl. 55 (1976), 743–756.CrossRefGoogle Scholar
(3)Nelson, E.Notes on non-commutative integration. J. Functional Analysis 15 (1974), 103–116.CrossRefGoogle Scholar
(4)Sakai, S.C*-algebras and W*-algebras (Berlin, Heidelberg, New York, Springer-Verlag, 1971).Google Scholar
(5)Segal, I. E.Anon-commutative extension of abstract integration. Ann. of Math. 57 (1953), 401–457; 58 (1953), 595–596.CrossRefGoogle Scholar
(6)Segal, I. E.Tensor algebras over Hilbert spaces. II. Ann. of Math. 63 (1956), 160–175.CrossRefGoogle Scholar
(7)Segal, I. E.Algebraic integration theory. Bull. Amer. Math. Soc. 71 (1965), 419–489.CrossRefGoogle Scholar
(8)Yosida, K.Functional analysis (Berlin, Heidelberg, New York, Springer-Verlag, 1968).CrossRefGoogle Scholar